Математика \ Вычислительная математика

Численное интегрирование. Анализ алгоритма функции SdxEpsilon, страница 2

4     64   2.01750201   2.00097833  -0.01652368

5    128   2.00097833   2.00005955  -0.00091878

6    256   2.00005955   2.00000370  -0.00005585

7    512   2.00000370   2.00000023  -0.00000347

8   1024   2.00000023   2.00000001  -0.00000022

9   2048   2.00000001   2.00000000  -0.00000001

Интеграл = 2

5.Задание:

С помощью функции SdxLaguerre(), SdxInfinity() вычислить интегралы

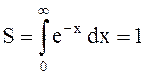      и          .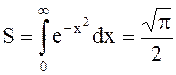

Для функции SdxLaguerre() построить зависимость погрешности вычисления одного из интегралов от nв пределах от 1 до 10.

Для функции SdxInfinity() нарисовать блок-схему алгоритма. Построить графики подынтегральной функции и выбрать необходимые параметры b0 и c.

Программа:

// Программа для расчета интегралов

// с помощью функции SdxLaguerre()

#include <iostream.h>

#include <conio.h>

#include <math.h>

#include "integral.h"

double F1(double x);

double F2(double x);

void main()

{

// описание данных

int n;

double S;

// ввод входных данных

n=10;

// обращение к функции

S=SdxLaguerre(F1,n);

// вывод результата

clrscr();

cout<<"Интеграл = "<<S<<endl;

getch();

}

double F1(double x)

// первая подынтегральная функция

{

return exp(-x);

}

double F2(double x)

// вторая подынтегральная функция

{

return exp(-x*x);

}

Результат выполнения программы:

Интеграл = 1

SdxLaguerre()–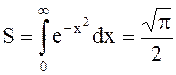 

Результат выполнения программы:

Интеграл = 0.886556

График зависимости погрешностей от n ( SdxLaguerre())

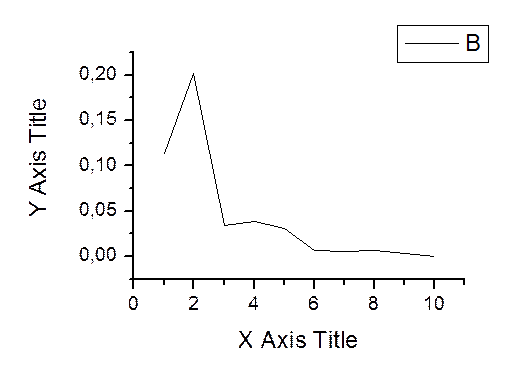
Таблица зависимости погрешностей от n:

n

SdxLaguerre() 

1

0.113773

2

0.20176

3

0.034677

4

0.038548

5

0.030444

6

0.007081

7

0.005155

8

0.006369

9

0.003239

10

0.000329

График подынтегральной функции   :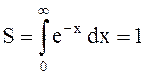

График подынтегральной функции   :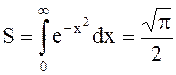

Возьмём в обоих случаях:   b0 = 0.05;  c = 1

// Программа для расчета интегралов

// с помощью функции SdxInfinity()

#include <iostream.h>

#include <conio.h>

#include <math.h>

#include "simpson.h"

double F1(double x);

double F2(double x);

void main()

{

// описание данных

int n,keyDemo;

double a,b0,c,eps,S;

// ввод входных данных

a=0;

b0=2 ;

c=1 ;

eps=1E-07;

keyDemo=1;

// обращение к функции

clrscr();

S=SdxInfinity(F1,a,b0,c,eps,keyDemo);

// вывод результата

cout<<endl;

cout<<"Интеграл = "<<S<<endl;

getch();

}

double F1(double x)

// первая подынтегральная функция

{

return exp(-x);

}

double F2(double x)

// вторая подынтегральная функция

{

return exp(-x*x);

}

Результат выполнения программы:

SdxInfinity()   –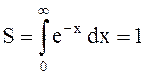 

1   0.10000000   0.04877058   0.09516258   0.04639201

2   0.20000000   0.09516258   0.18126925   0.08610667

3   0.40000000   0.18126925   0.32967995   0.14841071

4   0.80000000   0.32967995   0.55067104   0.22099108

5   1.60000000   0.55067104   0.79810348   0.24743245

6   3.20000000   0.79810348   0.95923780   0.16113431

7   6.40000000   0.95923780   0.99833844   0.03910065

8  12.80000000   0.99833844   0.99999724   0.00165880

9  25.60000000   0.99999724   1.00000000   0.00000276

10  51.20000000   1.00000000   1.00000000   0.00000000

Интеграл = 1

SdxInfinity()   –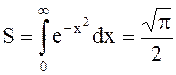 

1   0.10000000   0.04995836   0.09966766   0.04970930

2   0.20000000   0.09966766   0.19736503   0.09769737

3   0.40000000   0.19736503   0.37965284   0.18228781

4   0.80000000   0.37965284   0.65766986   0.27801702

5   1.60000000   0.65766986   0.86526623   0.20759637

6   3.20000000   0.86526623   0.88622158   0.02095536

7   6.40000000   0.88622158   0.88622693   0.00000534

8  12.80000000   0.88622693   0.88622693   0.00000000

Интеграл = 0.886227

6.Задание:

На основе сплайн-интерполяции подынтегральной функции вычислить интеграл 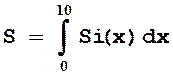 от подынтегральной функции, заданной таблично. Ее табличные данные находятся в файле si.dat. Построить график подынтегральной функции и оценить по нему правильность вычисления интеграла.

Программа:

// программа для вычисления интеграла от таблично заданной функции

// с помощью функции SdxSpline

#include <iostream.h>

#include <conio.h>

#include "spline.h"

#include "datafile.h"

void main()

{

// описание данных

int i,n,m,Err;

double S;

Vector A,B,C,D;

LVector X,Y;

// ввод входных данных

clrscr();

OutMessage("Вводим данные из файла. <Enter>");

Read2Vec(n,X,Y,1);

// сдвиг элементов массива

for (i=1; i<=n; i++)

{

X[i-1]=X[i];

Y[i-1]=Y[i];

}

m=n-1;

// интерполяция

Err=SplineCoeff(m,X,Y, A,B,C,D);

clrscr();

cout<<"Сплайн-интерполяция выполнена."<<endl;

cout<<"Err = "<<Err<<endl<<endl;

// вывод в файл программы подынтегральной сплайн-функции

cout<<endl;

WriteSpline(m,X,A,B,C,D);

// вычисление интеграла

cout<<endl;

S=SdxSpline(m,X,A,B,C,D);

cout<<endl;

cout<<"Интеграл = "<<S<<endl;

getch();

}

Результат выполнения программы:

Скачать файл