Стабилизация частоты вращения рабочего органа машины при различных фиксированных моментах нагрузки, страница 4

Рис. 7Схема включения тахогенератора

Коэффициент усиления разомкнутой системы К_р.тр , обеспечивающий в замкнутой системе требуемую статическую ошибку d_тр = 1.2% и диапазон регулирования Д = 20, определяется по [4.стр.14]:

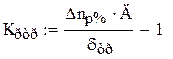
где Dn_р% - статическая ошибка разомкнутой системы тиристорный преобразователь-  двигатель.

Статическая ошибка разомкнутой системы ТП-Д из [6,стр.101]:

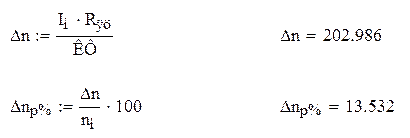
Тогда:

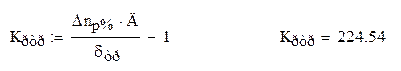
Коэффициент усиления промежуточного усилителя:

Определяем максимальную величину задающего напряжения U_зmax. Эта величина определяется из равенства:

При этом напряжении будет осуществляться стабилизация скорости потому, что рассогласование равно нулю. Регулирование скорости двигателя будет осуществляться при уменьшении  U_з < U_зmax.

7  Принципиальная упрощенная схема нескорректированной САУ

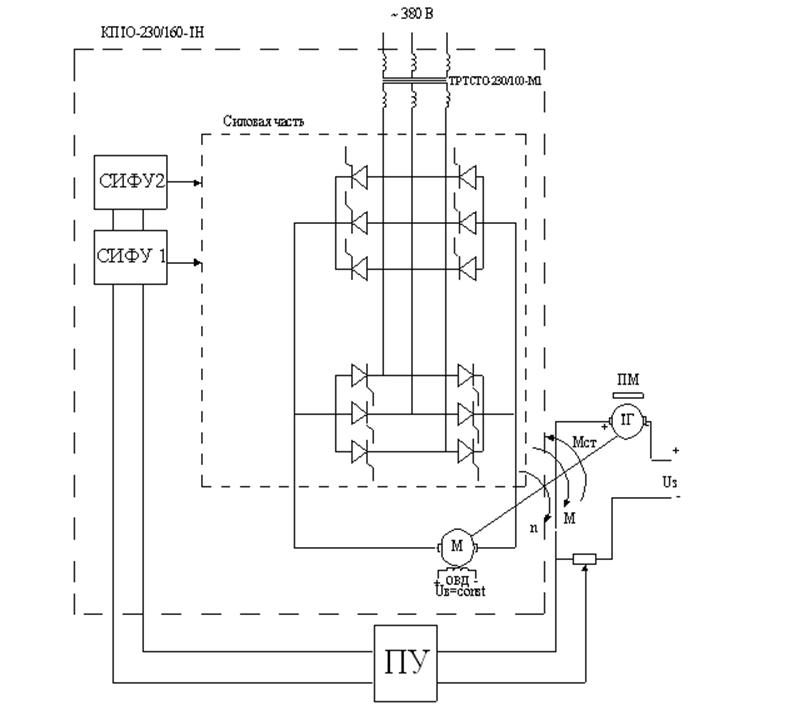
Рис. 8Принципиальная упрощенная схема нескорректированной САУ

ТР- силовой трансформатор ТСТО-230/100-М1

ТП - тиристорный преобразователь

ПУ - промежуточный усилитель

ТГ - тахогенератор ТМГ- 30П

D - двигатель постоянного тока П52

8  Расчет динамики САУ

8.1. Определение передаточных функций разомкнутой и замкнутой САУ по управляющему, возмущающему воздействиям и по ошибке

Представим структурную схему САУ [4,стр.18]:

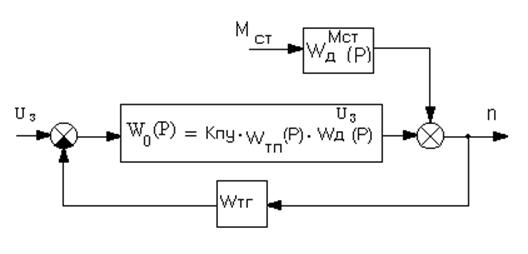
Рис. 9Структурная схема САУ для определения передаточной функция по управляющему воздействию

Уравнение замыкания САУ: 

e(p) = U_з(р) - U_тг(р)

Уравнение замкнутой САУ:

Получилась система уравнений:

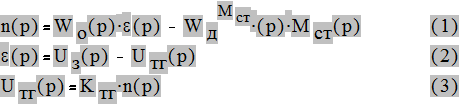
Подставляя (2) и (3) в (1) получим:

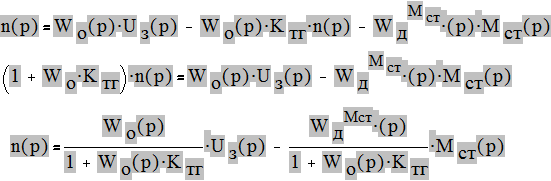
Передаточная функция замкнутой САУ по управляющему воздействию:

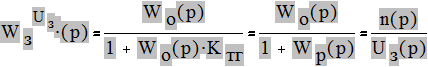
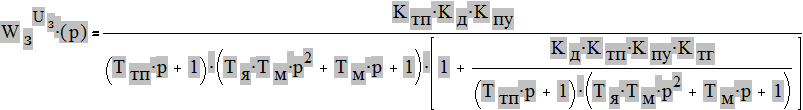
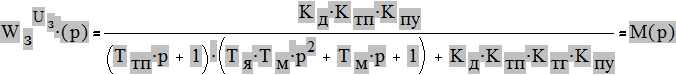
Передаточная функция замкнутой САУ по возмущению:

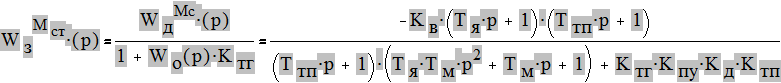
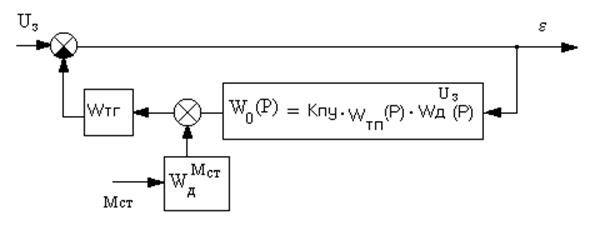
Рис. 10Структурная схема САУ для определения передаточной функция по ошибке

Передаточная функция замкнутой САУ по ошибке:

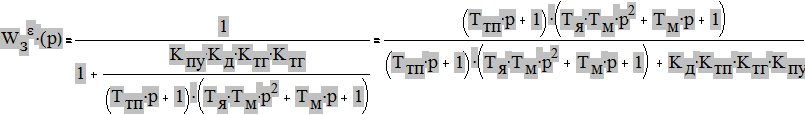
8.2  Оценка качества переходного процесса по логарифмической и амплитудно-частотной характеристикам разомкнутой системы

Передаточная  функция разомкнутой системы:

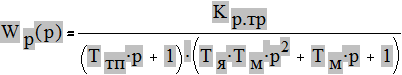
Система состоит из трех звеньев: усилительного, апериодического, звена второго порядка. Так как в звене второго порядка коэффициент демпфирования равен:

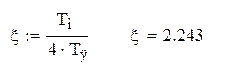
значит двигатель может быть представлен как два апериодических звена [4,стр.21].

Тогда передаточная функция разомкнутой системы:

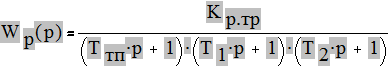
Постоянные времени апериодических звеньев:

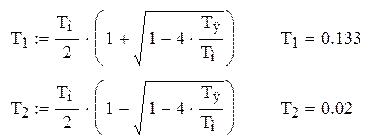
Уравнение ЛАХ системы L_нс(w) = åL_j(w)

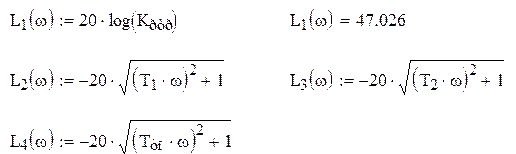
Построение ЛАХ осуществляем с помощью метода асимптот. Находим частоты сопряжения:

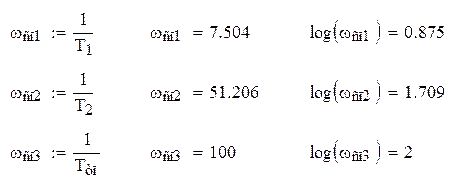
Уравнение ФЧХ системы:  Q_нс(w) = åQ_j(w)

Задаваясь значениями w находим  Qнс(w) и Qj(w):

w	0.01	0.1	1	10	100	1000
lgw	-2	-1	0	1	2	3
Qнс(w)	-0.093	-0.933	-9.283	-69.878	-193.594	-260.928

Анализ ЛАХ и ФЧХ показывает, что система неустойчива так как ФЧХ пересекает линию   -p в области опасных модулей. Система нуждается в коррекции.

8.3  Последовательная коррекция переходного процесса

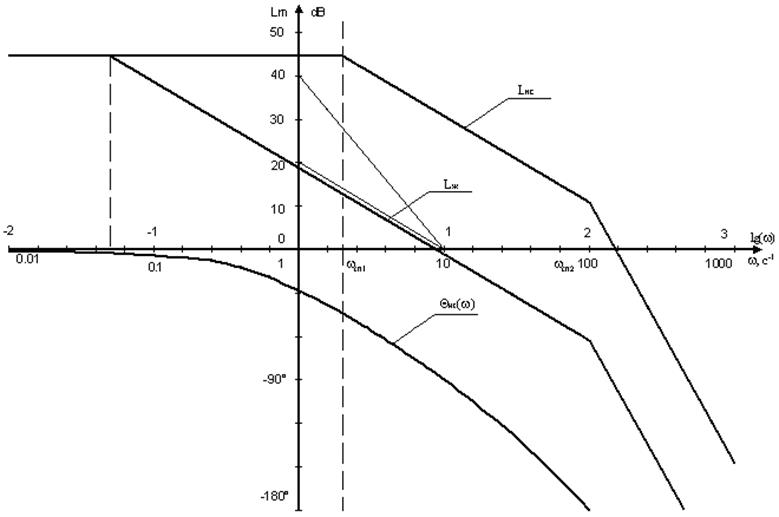
8.3.1 Построение желаемой ЛАХ САУ

По заданным показателям качества переходного процесса t_пп = 1 c, s_тр = 30%, М = 1.1 строим желаемую ЛАХ L_ж(w) = L_ск(w).

Для  того что бы построить желаемую ЛАХ определим ее частоту среза по [5,стр.4]:

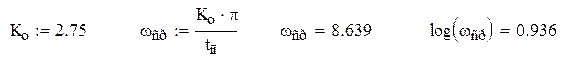
где Ко - коэффициент, который выбирается по рис.1 в [5,стр.4]

Проводим через точку w_ср прямую с наклоном -20 Дб/дек до пересечения с L_нс(w) в низкочастотной области, получим частоту сопряжения:

В высокочастотной области для получения наиболее простого корректирующего устройства желательно что бы наклон желаемой ЛАХ совпадал с наклоном ЛАХ нескорректированной системы. Частоты сопряжения в высокочастотной области:

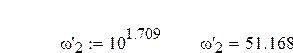
8.3.2. Расчет параметров корректирующей цепи.

ЛАХ корректирующего устройства: L_к(w) = L_ск(w) - L_нск(w).

Вычитаем ординаты ЛАХ нескорректированной системы из ординат ЛАХ скорректированной системы получаем ординаты ЛАХ корректирующего устройства.