Обобщенными координатами называют совокупность параметров, достаточных для однозначного определения положения точек механической системы в любой момент времени. Производная от обобщенной координаты перемещения дает обобщенную скорость. Обобщенной силой называют величину, произведение которой на бесконечно малое приращение соответствующей обобщенной координаты равняется сумме элементарных работ, совершенных силами, приложенными к системе, на ее перемещение, обусловленном указанным приращением обобщенной координаты. Например, при вращательном движении обобщенной координатой может быть угол поворота, обобщенная скорость – это угловая скорость, обобщенные силы – это моменты, приложенных сил относительно оси вращения.
Механические связи и их классификация. Механические связи делятся на свободные и несвободные. Если каждая точка системы может занять любое положение в пространстве и иметь любую скорость, то такую систему называют свободной. Если на движение точек и тел наложены в пространстве ограничения, то система не свободна. Ограничения, не позволяющие точкам или телам системы занимать произвольные положения или приобретать произвольные скорости, называются связями. Связи могут быть удерживающими и неудерживающими. Если связь аналитически записывается уравнением, то она – удерживающая. Если связь записывается неравенством, то она – неудерживающая. Например, две материальные точки соединены жестким невесомым и нерастяжимым стержнем. Эта связь будет удерживающей. Если стержень заменить гибкой и нерастяжимой нитью, то связь станет неудерживающей. Если связь не зависит от времени, то она носит название стационарной. Если связь зависит от времени, т. е. параметр времени входит в уравнения, описывающие эти связи, то она носит название нестационарной. Если связи не ограничивают скорость, т. е. фиксируют только положение, то они называются голономными или геометрическими. Если связи ограничивают скорости точек механической системы, то связи называются голоном Кинематическая передача изменяет количественные параметры механической энергии, а также характер движения исполнительных органов, т.е. преобразует поступательное движение во вращательное и наоборот. Кинематические передачи делятся на два класса: линейные и нелинейные. В линейных передачах соотношения между параметрами механической энергии ее источника (электродвигателя) и механизма (рабочей машины) остаются неизменными и обусловлены конструкцией передачи. В нелинейных передачах соотношения между параметрами механической энергии ее источника и механизма являются функцией какого-нибудь параметра движения, например, угла поворота, или времени.
По конструктивному исполнению кинематические передачи делятся на редукторы, ременные и клиноременные передачи, барабан-тросс, шкиф-канат, винт-гайка, зубчатое колесо-рейка, шарнирные передачи типа кривошипно-ползунного и кулисного характера.
Редукторы — это зубчатые передачи, которые находятся в едином корпусе. Они могут быть одноступенчатыми, двухступенчатыми, n-ступенчатыми. Одно из изображений редуктора на рис. 1:
![]()
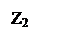
![]()
![]()
![]()
![]()
![]()
![]()

![]()
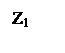
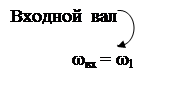

![]()
По принципу действия редукторы подразделяются на обычные и планетарные. При передаче механической энергии от ее источника к технологической машине и обратно существуют в кинематических передачах потери этой механической энергии. Потери оцениваются КПД редуктора (ŋмех), значение которого зависит от количества передаваемой механической энергии. Редуктор кроме этого характеризуется передаточным числом
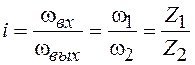
где ω1 — скорость входного вала, ω2 — скорость выходного вала,
Для
многоступенчатого редуктора передаточное число равно произведению передаточных
чисел отдельных ступеней ![]() .
.
Уравнение движения электропривода
Механическая часть электропривода представляет собой систему твердых тел, на движение которых наложены ограничения, определяемые механическими связями. Уравнения механических связей устанавливают соотношения между перемещениями тел в системе. В механике такие связи носят название голономные, другими словами, если механические связи не ограничивают скорость, а только фиксируют положение, то они голономные, т. е. геометрические связи. В системах с голономными связями число независимых переменных, т.е. обобщенных координат, определяется числом степеней свободы данной системы. Для таких систем, поведение которых описано ДУ, наиболее общей формой записи является уравнение Лагранжа 2-го рода в обобщенных координатах:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.