Механическая часть электромеханической системы. Нагрев и охлаждение электродвигателей. Шаговый двигатель как элемент электромеханической системы, страница 14

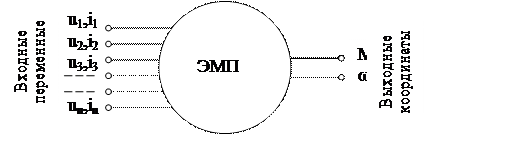
В структуре электромеханической системы электромеханический преобразователь (электродвигательное устройство, электрическая машина) является функциональным звеном, в котором выполняется электромеханическое преобразование энергии. Качественные показатели электропривода (регулировочные свойства, способы управления, энергетические показатели) определяются физическими свойствами электромеханического преобразователя. В структурной схеме он представлен двигателем, ротор которого не обладает механической инерцией, не имеет механических потерь и жестко связан с реальным ротором, входящим в состав механической части электропривода, т.е. идеализированным. Эти условия позволяют сопоставить ему электромеханический многополюсник, имеющий N входных переменных и две выходные координаты: электромагнитный момент М, развивающийся при скорости ω, рис. 1. Электромагнитный момент является входной переменной для механической части электропривода. Скорость ω определяется условиями движения механической части. Эти выходные координаты электромеханического преобразователя связывают его с механической частью в единую взаимодействующую систему.

Электрические двигатели в основном многофазные машины. Это обстоятельство осложняет математическое описание динамических процессов, в силу того, что с увеличением числа фаз возрастает число уравнений электрического равновесия, усложняются электромагнитные связи. Для упрощения математического описания поведения электрических машин при изучении их различных режимов работы целесообразно перейти к эквивалентной двухфазной модели этой машины, которую еще называют обобщенной электрической машиной. При выполнении такой процедуры подразумеваются следующие допущения:

– витки обмоток статора и ротора при равенстве их полных сопротивлений фаз синусоидально распределены в пространстве машины,

– машина симметрична, т. е. обмотки имеют одинаковое число витков, сдвинутых на 90⁰, а воздушный зазор машины гладкий и равномерный,

– магнитная цепь машины ненасыщена, а энергия магнитного поля сосредоточена в воздушном зазоре машины.

Схема обобщенной электрической машины приведена на рис.    .

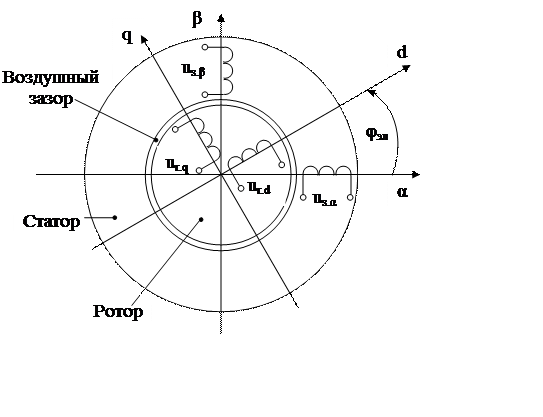Уравнения электрического равновесия (уравнения Кирхгофа) выраженные через потокосцепления имеют вид

.

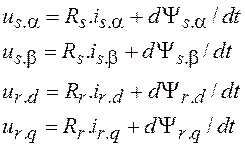где  u_s.α, u_s.β, u_r.d, u_r.q, i_s.α, i_s.β, i_r.d, i_r.q – соответственно напряжения и токи в обмотках статора (s) и ротора (r) по осям статора (α – β) и ротора (d – q), R_s, R_r – активное сопротивление обмотки статора и приведенное активное сопротивление обмотки ротора, Ψ_s.α, Ψ_s.β, Ψ_r.d, Ψ_r.q, – соответствующие потокосцепления статора и ротора.

Полученные уравнения при исследованиях работы электрической машины необходимо решать совместно. Для этой цели их следует привести к одной системе координат Приведение уравнений  может быть выполнено к следующим системам координат:

– к системе координат, жёстко связанной с осями обмоток статора (сист. координат статора);

– к системе координат, жёстко связанной с осями обмоток ротора (сист. координат ротора);

– к системе координат, жёстко связанной с осью вращ. магнитного поля статора или ротора;

– к системе координат, вращающейся с произвольной скоростью.

Выбор системы координат определяется целями и задачами изучения исследования того или иного типа электропривода. . Рассмотрим первый вариант системы – систему координат, жёстко связанной с осями обмоток статора В этой системе результирующий вектор тока, потокосцепления или напряжения можно разложить на составляющие в направлении осей координат, неподвижных в пространстве, т.е. жёстко связанных с осью какой-либо из обмоток статора электрической машины. Эти оси принято обозначать a и b. При этом целесообразно вещественную ось a совместить с направлением оси обмотки, например фазы А. Тогда в любой момент времени вектор тока статора можно определить через его составляющие по вещественной - a и мнимой – b осям, т.е.

,    или       и     Следовательно, магнитное поле, создаваемое током , можно рассматривать как сумму двух полей, создаваемых токами в двух обмотках, расположенных взаимно перпендикулярно в осях a и b. Установим связь между составляющими a, b и мгновенными значениями фазных токов трёхфазной машины. Для составляющей тока по оси a имеем, при условии :