Разработка составов масс для производства клинкерного кирпича, отвечающего требованиям ТУ ВУ 300035579.403 – 2005 на основе белорусского и украинского сырья (Экспериментальная часть дипломного проекта), страница 10

При статистической обработке группы результатов наблюдений следует выполнить следующие операции.

1) Определение среднего арифметического х по формуле:

                                                  х = 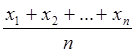,                                             (3.3)

где х₁, х₂ …х_n – случайные значения определяемой величины;

n – число опытов.

2) Определение отклонений измеряемой величины от ее среднего арифметического для каждого опыта (x - x_i).

3) Определение квадрата отклонения случайной величины от ее значения

(x - x_i)².

4)Определение среднеквадратичного отклонения δ по формуле:

Δ = S (x)= 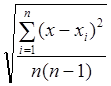,                                           (3.4)

5) определение коэффициента Стьюдента при данной доверительной вероятности Р_g = 0,95 [16].

6) определение величины доверительного интервала проводится по формуле:

= t_рδ,                                                      (3.5)

где t_р–коэффициент Стьюдента, который зависит от числа измерений и величины доверительной вероятности Р_g.

Относительная погрешность, ε, % определяется по формуле:

ε =                                                         (3.6)

За результат измерения принимаем среднее арифметическое результатов измерений, в которые предварительно введены поправки для исключения систематической погрешности.

В качестве примера проведем обработку результатов измерения прочности при изгибе образцов составов К7, К8, К9, данные которых приведены в              таблице 3.7.

Таблица 3.7 − Результат измерения прочности при изгибе

Данные статистической обработки занесем в таблицу 3.8.

Таблица 3.8 − Статистическая обработка данных для образцов состава К9

Продолжение таблицы 3.8

Определим среднее арифметическое  по формуле (3.3).

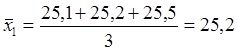МПа;

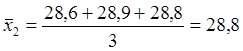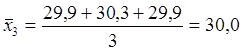МПа;

МПа.

В таблице 3.9 представлены средние арифметические значения для остальных составов.

Таблица 3.9 − Среднее арифметическое значение прочности при изгибе образцов составов К7-К9

Далее определяем среднеквадратичное отклонение для состава  К9 по  формуле (3.4).

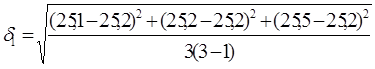= 0,13 МПа;

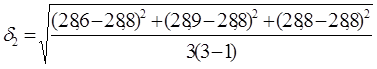= 0,09 МПа;

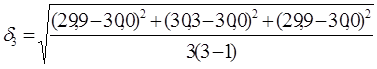= 0,14 МПа.

Результаты расчета среднеквадратичного отклонения значений приведены в таблице 3.10.

Таблица 3.10 − Среднеквадратичное отклонение значений прочности