Статистические характеристики в формировании системы показателей статистики связи. Анализ рядов динамики показателей связи. Кореляционно-регрессионный анализ и его использование при изучении взаимосвязей

2. Статистика.

2.1.Статистические характеристики в формировании системы показателей статистики связи (относительные, средние величины) (Задачи 5 шт).

Статистический показатель представляет собой обобщенную количественную характеристику социально-экономических явлений и процессов в единстве с их качественной определенностью. В зависимости от метода исчисления статистические показатели делятся на абсолютные, относительные и средние величины.

Абсолютные статистические величины выражают размер или объем изучаемого явления в определенных границах. Большое значение в статистике имеют относительные величины, которые используют для сравнительной оценки явлений общественной жизни. Относительная величина - числовая мера сравнения двух статистических величин и определяется отношением одного абсолютного показателя к другому.

Средняя величина – это есть статистический показатель, характеризующий какое-то явление или процесс. Для определения ср.величины используется следующее отношение:

Ср.величина = объем варьирующего признака / Объем совокупности,

(З = ФОТ / Т, где З – ср.зарплата; ФОТ – фонд оплаты труда; Т – численность работников).

Средняя арифметическая.

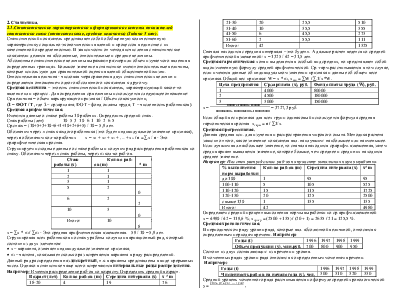
Имеются данные о стаже работы 10 рабочих. Определить средний стаж.

Стаж работы (лет)                10  5  3  10  6  1  10  2  6  5

Ср.стаж = (10+5+3+10+6+1+10+2+6+5) / 10 = 5,8 лет.

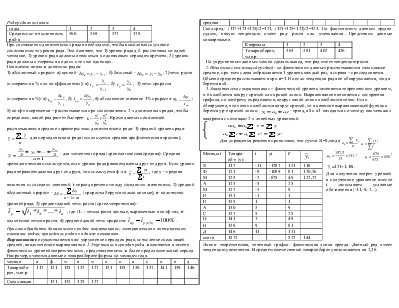
Обозначим через х стаж каждого работника (это будет индивидуальное значение признака), через n обозначим кол-во рабочих        x = х₁ + х₂ + х₃ + … + х_n / n = åх / n - Это ср.арифметическая простая.

Сгруппируем исходные данные о стаже работы и получим ряд распределения работников по стажу. Обозначим через х стаж работы, через m кол-во раб-ов.

х = åх * m / åm - Это средняя арифметическая взвешенная.   58 / 10 = 5,8 лет.

Сгруппировав всех работников по стажу работы получили вариационный ряд, который состоит из двух элементов:

·  х – варианта, означает индивидуальное значение признака;

·  m – частота, показывает сколько раз встречается варианта в ряду распределений.

Данный ряд распределения наз.дискретный, т.к. варианты представлены в виде прерывных чисел. Однако в статистике чаще всего встречаются интервальные ряды распределения.

Например: Имеется распределение раб-ов по возрасту. Определить средний возраст.

Сначала находится середина интервала – это будет х. А дальше расчет ведется по средней арифметической взвешенной: х = 1325 / 42 = 31,5 лет.

Средняя гармоническая хотя и выделяется в особый вид средних, но представляет собой видоизмененную формулу средней арифметической. Ср.-гарм.рассчитывается в том случае, если имеются данные об индивидуальном значении признака и данные об общем весе признака. Общий вес признака: W = х * m, х_взв = åW / å1/х *W.

х =                       ^{80000 + 180000 + 150000}              = 3727,3 руб.

                 ^{80000/4000 + 180000/4500 + 150000/3000}

Если общий вес признака для всех групп одинаковый используется формула средняя гармоническая простая  х_гарм = n / å1/х.

Средняя прогрессивная.

Данная средняя исп. для изучения и распространения мирового опыта. Методика расчета зависит от того, какое значение показателя явл. наилучшим: наибольшее или наименьшее. Если лучшим явл.наибольшее значение, то сначала находится ср.арифм.взвешенная, затем среди вариант выявляется значение, которое больше, чем среднее и среди них находится среднее значение.

Например: Имеется распределение раб-ов по проценту выполнения норм выработки.