______________
Для вариационного ряда: σ = √∑(х - хср)²m / ∑m
- дисперсия - квадрат σ.
Для первичного ряда: σ² = ∑(х - хср)² / n
Длявариационного ряда: σ² = ∑(х - хср)²m / ∑m
- коэффициент вариации – показывает, на сколько % в среднем отклоняется каждое значение признака от средней величины; характеризует степень однородности совокупности: если к-т вариации > 33%, то совокупность неоднородная, а средняя нетипична для данной совокупности и не может быть использована в дальнейших расчетах.
Чтобы сделать совокупность однородной, надо разбить ее на однородные типические группы и в каждой группе рассчитать свою среднюю.
V = (σ / хср) *100%
Cвойства дисперсии:
1. Если все варианты увеличить в какое-то число раз, то дисперсия увеличится в квадрат этого числа.
σ1 = ∑(хa - хсрa)²m / ∑m = a²∑(х - хср)²m / m = a²σ²
2. Если варианты увеличить или уменьшить на какое-то число, то дисперсия от этого не изменится.
σ1² = ∑(х+a – хср-a)²m / ∑m = σ²
3. Если все частоты увел-ть в какое-то число раз, то дисперсия от этого не изменится.
σ1² = ∑(х – хср)²mk / ∑mk = k∑(х – хср)²m / k∑m = σ²
4. Правило сложения дисперсии – используется в том случае, если изучаемая совокупность разделена на группы. В каждой группе рассчитывается дисперсия, далее находится средняя из групповых дисперсий.
σср² = ∑(σi²mi) / ∑mi
Далее определяется межгрупповая дисперсия:
δ² = ∑(хсрi – хсробщ)²mi / ∑mi
Далее рассчитывается общая дисперсия:
σ²общ = σср² + δ² - правило сложения дисперсии
Показатели ассиметрии
Между частотами и вариантами существуют следующая закономерность: с увеличением вариант частоты увеличиваются, достигают max, а потом снижаются. Это называется закономерностью распределения.
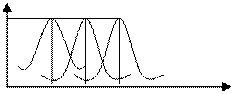 m
m
x
М0 хсрМ0 М0
Особенностью этой кривой явл-ся то, что она симметрична. Однако на практике симметричное распределение встречается очень редко. В больш-ве случаев распределение бывает несимметричное.
Для оценки степени асимметрии рассчитываются след. показатели:
1. Коэф-т асимметрии: Кас = (Хср – М0) / σ
Если Кас > 0, то асимметрия правосторонняя, если Кас < 0 –левосторонняя,если Кас = 0 – то симметричная.
2. Эксцесс - Еs - характеризует островершинность или плосковершинность распределения.
Еs = (М^4 / σ^4) – 3
М^4 = ∑(х - хср)^4 m/ ∑m – момент 4-го порядка
Если Еs > 0, распределение островершинное, если Еs < 0 – плосковершинное.
2.7 Применение выборочного метода наблюдения в статистике связи (Теория)
Выборочное наблюдение является одним из видов несплошного наблюдения. При выборочном наблюдении обследованию подвергаются не все единицы изучаемой совокупности, а только часть их, отобранная в случайном порядке. Полученные обобщенные показатели распространяются на всю изучаемую совокупность. При проведении выборочного наблюдения возникают ошибки выборки в связи с тем, что обследованию подвергаются только часть единиц совокупности, которая по структуре может отличаться от всей совокупности. Выборочные характеристики в виде средних и относительных величин отличаются от аналогичных характеристик в генеральной совокупности на величину ошибки выборки. При организации выборочного наблюдения стремятся к тому, чтобы ошибка выборки была минимальной. Размер ошибки выборки зависит от объема выборки, от вариации значений признаков, а также от способа отбора единиц, образующих выборочную совокупность.
Задачи, которые возникают при организации выборочного обследования можно разделить на два вида:
1. Определение среднего размера признака.
2. Определение доли единиц, обладающих данным признаком.
Выборка бывает бесповторной и повторной. Если отобранная единица или целая серия не возвращается в совокупность, то она называется бесповторной. Если одна и та же единица попадает в выборку несколько раз, такая выборка называется повторной.
По способу отбора единиц для обследования различают следующие виды выборки: собственно-случайная, типическая, серийная, механическая. Собственно-случайная, типическая и серийная выборки могут быть повторными и бесповторными.
Билет 2.8 Способы определения ошибки репрезентативности при различных видах отбора в выборочном наблюдении (Задача вариантов 6)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.