Статистические характеристики в формировании системы показателей статистики связи. Анализ рядов динамики показателей связи. Кореляционно-регрессионный анализ и его использование при изучении взаимосвязей, страница 4

Скол.сред.: (117+121+125)/3=121, (121+125+123)/3=123. По фактическим данным трудно судить, какую тенденцию имеет ряд: роста или уменьшения. Представим данные поквартально.

По укрупненным данным можно сделать вывод, что ряд имеет тенденцию роста.

2.Исчисление скользящей средней- по фактическим данным рассчитываются скользящие средние, при этом слева отбрасывается 1 уровень каждый раз, а справа – присоединяется. Обычно среднее рассчитывается при n=3. Но если тенденция ряда не обнаруживается, тогда берется n=5.

3.Аналитическое выравнивание – фактический уровень заменяется теоретическим уровнем, к-й колеблется вокруг прямой или кривой линии. Выравнивание начинается с построения графика, по которому определяется, вокруг какой линии колеблются точки. Если обнаружено, что точки колеблются вокруг прямой, то в качестве выравнивающей функции берется ур-е прямой линии: - трэнд, а0 и а1  находятся по методу наименьших квадратов с помощью 2-х линейных уравнений:

.

Для упрощения решения принимают, что сумма St=0,тогда , ;

, ; =131+1,18t.

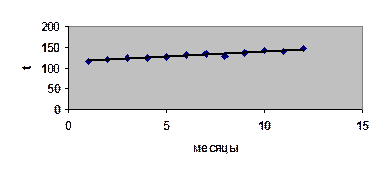
Для получения теорет. уровней в полученное уравнение вместо t записываем условные обозначения (-11,-9,-7...).

Линия- теоретическая, точечный график- фактическая линия тренда. Данный ряд имеет тенденцию увеличения. В среднем ежемесячный товарооборот увеличивается на 2,36.

Интерполяция – получение промежуточных значений динамического ряда, которые по каким-либо причинам оказались неизвестными. 1) Средняя арифметическая из соседних уровней ряда: ; 2) По абсолютному приросту, ; ; 3) По среднегодовому темпу роста: 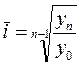, где n- количество уровней; .

Экстраполяция – определение уровней ряда на последующий период (прогноз). 1)По среднему абсолютному приросту: , n-кол-во уровней ряда; m – кол-во прироста; ; 2) По среднему темпу роста: ; 3) По аналитическому выравниванию – в полученное уравнение прямой вместо t подставляется след-е условное обозначение, к-е идет за последним уровнем.

Приведение рядов к одному основанию используется для сравнения двух динамических рядов. Для этого каждый уровень каждого динамического ряда сравнивается с начальным уровнем данного ряда и выявляется, какой ряд растет быстрее.

Изучение сезонных колебаний – многие динамические ряды подвержены сезонным колебаниям, т.е. в одни месяцы уровни ряда резко возрастают, а в другие резко падают. Для оценки степени сезонности в динамическом ряду рассчитываются показатели: 1) индекс сезонности: 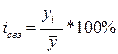- данной формулой можно пользоваться, только если сред. уровень ряда из года в год практически не меняется или меняется, но незначительно. Инач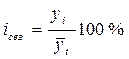е: ,где -теорет. уровни, полученные по аналит. выравниванию ;  2) Среднее квадратическое отклонение: - рассчитывается за ряд лет и выясняется, в каком году были наибольшие сезонные колебания.