fnp=fhl=fo(l+iε), (1)
где i=![]() - безразмерная координата
рассматриваемого слоя при условии равномерной плотности по высоте;
- безразмерная координата
рассматриваемого слоя при условии равномерной плотности по высоте;
ε=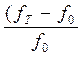 - коэффициент,
характеризующий физико-механические свойства сыпучего тела. По данным В.В.
Гортинского [2], для пшеницы и продуктов ее измельчения y
- коэффициент,
характеризующий физико-механические свойства сыпучего тела. По данным В.В.
Гортинского [2], для пшеницы и продуктов ее измельчения y![]() =(
=(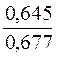 );
);
ε =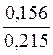 при
средних размерах частиц продукта соответственно,
при
средних размерах частиц продукта соответственно, ![]() мм
и влажности 13,5 %.
мм
и влажности 13,5 %.
При принятой схеме сдвигового течения зерна можно считать, что условия движения отдельных масс данного элементарного слоя одинаковы по всей неограниченной протяженности этого слоя. Следовательно, массу элементарного слоя , отнесенную к единице площади решета, можно рассматривать как движение материальной частицы.
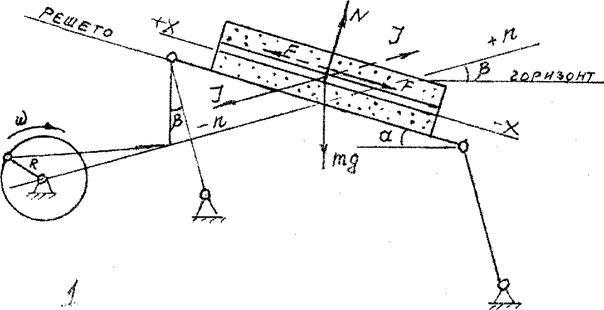
Рис. 1. Схема сил, действующих на элементарный слой при его относительном движении
![]() На рисунке 1 дана схема сил,
действующих на элементарный слой зерна при его относительном движении внутри
зернового тела. Решето совершает в плоскости n-n
гармонические колебания с радиусом кривошипа R и частотой w= πn/30, где n - число
колебаний в минуту.
На рисунке 1 дана схема сил,
действующих на элементарный слой зерна при его относительном движении внутри
зернового тела. Решето совершает в плоскости n-n
гармонические колебания с радиусом кривошипа R и частотой w= πn/30, где n - число
колебаний в минуту.
В направлении
колебаний действует сила инерции J=mw![]() Rcoswt, возрастающая
до максимальной величины j
Rcoswt, возрастающая
до максимальной величины j![]() =w
=w![]() R при ускорении
решета
R при ускорении
решета
Разделим полный период колебания решета на правый и левый интервал, границей между интервалами является ускорение решета, равное нулю. В правом интервале сила инерции переносного движения направлена справа налево.
Правый интервал. Дифференциальное уравнение при движении зерна вверх по решету запишется:
тх = Jcos(β + α)-mgsinα- F, (3)
где F – Ntgφ=m[w2R cos wt sin(β +α)- g cosα]tgφ
Подставим значения в уравнение (3), получим
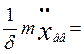 w
w![]() Rcoswt-g
Rcoswt-g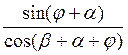 (4)
(4)
Второй член правой части уравнения (4) не зависит от времени. Обозначим его Р:
Р= g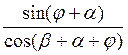 (5)
(5)
Предельное
ускорение относительного движения верхнего слоя зерна еще равно нулю при любых
углах поворота кривошипа, если соблюдается условие w![]() R=P:
R=P:
-для горизонтально направленных колебаний (а ≠ 0, β= 0)
P = gtg(α+φ); (6)
- в случае горизонтальной плоскости решета (α = 0, /β = 0)
P =gtgφ (7)
Левый интервал. Зерно движется вниз по решету. Сила инерции направлена слева направо. Дифференциальное уравнение относительного движения запишется как
тх= F - Jcos(β + α)-mg sinα, (8)
где J=mw2Rcoswt
F = mg[cosa + ksin(β + a)cos wt]gφ
Подставим значения в уравнение (8), получим
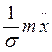
![]() =w
=w![]() Rcoswt-g
Rcoswt-g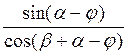 (9)
(9)
где σ=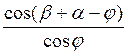
Правую часть уравнения (9) обозначим
|
(10) |
q=g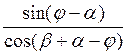 (10)
(10)
При w![]() R=q ускорение
относительного движения верхнего слоя зерна в левом интервале вниз по решету
равно нулю при любых углах поворота кривошипа, если соблюдаются условия:
R=q ускорение
относительного движения верхнего слоя зерна в левом интервале вниз по решету
равно нулю при любых углах поворота кривошипа, если соблюдаются условия:
- для горизонтально направленных колебаний (β =0), если
w2R = q = gtg(φ-a); (11)
- для горизонтальной плоскости решета (α=0, β = 0) w2R = q = gtgφ (12)
Графоаналитический способ определения энергии инерционного сдвигового течения зерновой среды при углах наклона и направлении колебаний плоского решетах равных нулю.
Графический способ определения параметров относительного движения зерна на плоском решете, совершающем гармонические колебания при углах наклона решета и направлении колебаний α=0, β = 0 , показан на рисунке 2.
Отложим от
поверхности зернового слоя толщину на решете Н![]() =2см и Н=4 см.
=2см и Н=4 см.
Ордината O'![]() -О' соответствует
верхнему и нижнему положению кривошипа на вертикальном диаметре окружности,
делит амплитуду колебания решета на две половины - правый и левый интервал
колебаний.
-О' соответствует
верхнему и нижнему положению кривошипа на вертикальном диаметре окружности,
делит амплитуду колебания решета на две половины - правый и левый интервал
колебаний.
Горизонтальная
линия, проходящая через точку O![]() , обозначает
нижний слой зерна, а также плоскость решета. От вертикальных линий [О' - О'; O
, обозначает
нижний слой зерна, а также плоскость решета. От вертикальных линий [О' - О'; O![]() - О; О" - О") вправо и
влево откладываются для верхнего и нижнего элементарных слоев величины связи
(трения) Fho=Oa, и Fнmax= O
- О; О" - О") вправо и
влево откладываются для верхнего и нижнего элементарных слоев величины связи
(трения) Fho=Oa, и Fнmax= O![]() в. Соединив
точки (а и в) прямой
линией, получим силу связи Fhi для любого
элементарного слоя.
в. Соединив
точки (а и в) прямой
линией, получим силу связи Fhi для любого
элементарного слоя.
Верхняя
горизонтальная линия, проведенная через точки О-О'
-О", обозначает верхний слой зерна. Максимальная величина силы
инерции для каждого элементарного слоя равна силе связи для данного слоя Ff=(mw![]() R)imax.
R)imax.
Перемещение частиц верхнего слоя зерна в относительном движении определяется по общепринятым дифференциальным уравнениям для материальной точки, поэтому относительно линии поверхности зерна О-О" построим графики скоростей и ускорений решета.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.