Схема сил, действующих на элементарный слой зерна при его относительном движении внутри зернового тела. Графический способ определения параметров относительного движения зерна на плоских решетах, страница 2

Рассмотрим два варианта относительного движения зерна при толщине слоя H=4см (1-й вариант) и толщине слоя H=2 см (2-й вариант), при этом поверхность зерна оставляем на месте. Параметры колебания решета не меняются, меняется лишь по высоте поверхность решета.

Исследуем относительное движение зерна при 1-м варианте.

Передача энергии от поверхности решета каждому следующему слою по высоте осуществляется через силы связи (трения) между элементарными слоями.

Сила связи для каждого слоя определяется из выражения

F_hi=yhgf (1+iε),                                                                            (13)

где yhg - давление приходящееся на 1см² от массы вышележащего слоя зерна,

γ-объемная масса зерна,

h-высота(см).

f (1+ iε )=f_np - приведенный коэффициент внутреннего трения зерна. Обозначения даны выше.

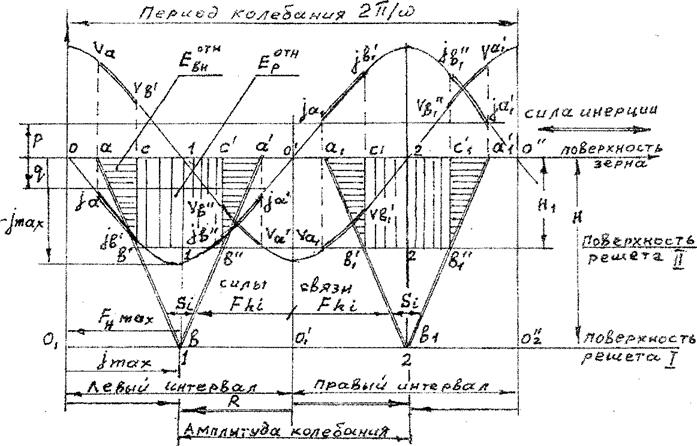
Рис. 2. Графический способ определения параметров относительного движения зерна на плоских решетах, совершающих гармонические колебания при углах наклона решета и направлении колебаний α=0, β = 0

Если принять изменение f_np по прямолинейному закону, то задача определения сил связи элементарных слоев и, следовательно, начала и конца сдвига каждого слоя сводится к отысканию двух точек: точки начала сдвигового течения (а) и начала сдвига нижнего слоя (в).

Положение точки (а) определится из выражения (7)

Оа = Р = g f  = 9,81 -0,65 = 6,37 м/с²

При ускорении решета w²R > 6,37 м/с² верхний слой начинает сдвигаться - отставать от нижележащего слоя зерна.Сила связи верхнего слоя зерна с нижележащим равна F=6,37•10Н.

Для общего случая, когда α≠0, β≠0 точки сдвига верхнего слоя в правом и левом интервалах движения будут несимметричны. Значения Р и q —определяются  по уравнениям (5) и (10).

Соединив все точки начала и конца сдвига верхнего слоя (точки а , а,а′, а) с точками начала и конца сдвига нижнего слоя (точки в,в), получим в правом и левом интервалах по две наклонных прямых (а-в и а′-в) и (а-ви а′- в) определяющих начало и конец сдвига каждого элементарного слоя.

Частный случай I

На рисунке 2 приведен простой вариант относительного движения зерна и решета - раскачивание всей зерновой массы относительно неподвижного нижнего слоя. Ускорение решета подобрано так, что в точке в сила сопротивления сдвигу нижнего слоя равна силе инерции слоя:

F_нmax=mwRmax

В данном случае нижний слой относительно решета остается неподвижным, в то время как каждый вышележащий слой перемещается на величину Si, обратно пропорциональную величине силы связи F.

Кинетическая энергия элементарного слоя dG в абсолютном движении в момент начала сдвига равна

hE=·,                                     (15)

где v- скорость начала сдвига и торможения данного элементарного слоя, определяемая на кривой скорости решета.

Эта энергия диссипатирует, превращаясь в работу сил трения внутри зерновой среды на границах элементарного слоя:

    

                                                                                     (16)

Суммарная площадь треугольников ава" и а_в_а_' является интегралом выражения (16) и с учетом масштаба выполненных построений показывает удельную (для зернового столба высотой Н и сечением 1 см²) внутреннюю кинетическую энергию, затрачиваемую на сдвиговое течение зерновой среды за полный период колебания решета.

                                     E·μ· μ·10Дж                      (17)