Другие предметы \ Автомобили

Автомобили. Проектирование и расчет рулевых управлений: Учебно-методическое пособие, страница 13

11. ПРОЧНОСТНОЙ РАСЧЕТ РУЛЕВОГО УПРАВЛЕНИЯ

Расчеты на прочность проводят по двум режимам:

-  по максимальному усилию, которое водитель может приложить к рулевому колесу;

-  по максимальному тормозному моменту на колесах.

Так как методы расчетов деталей рулевого управления на усталостную прочность разработаны недостаточно, расчеты носят сопоставительный характер, т. е. получаемые расчетные напряжения сравнивают с напряжениями в аналогичных деталях автомобиля, хорошо зарекомендовавших себя в эксплуатации.

Выполнение прочностного расчета базируется на материале, который приводится в дисциплинах "Детали машин", "Сопротивление материалов".

11.1. Расчет рулевых механизмов

Рулевой вал рассчитывают на кручение

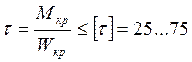 МПа,

где

Мкр

– крутящий момент на рулевом валу

,

Fр

– усилие, прикладываемое к рулевому колесу;

Rр

– радиус колеса;

Wкр

– полярный момент сопротивления.

Для сплошного вала

,

где

d

– наружный диаметр вала.

Для полого вала

,

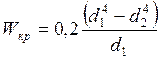где

d1 и d2

– соответственно внутренний и наружный диаметры.

Запас по пределу прочности

.

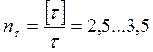Угол закручивания вала

,

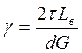где

Lв

– длина вала;

G

– модуль упругости второго рода.

При максимальном моменте на рулевом валу угол закручивания не должен превышать 5,5…7,5°.

В рулевых механизмах легковых автомобилей диаметр вала сошки dс = 23…32 мм, межосевое расстояние аw = 43…60 мм, а грузовых – аw = 66…90 мм.

Наиболее сильно изнашивающимся и наиболее сильно нагруженном местом рулевых механизмов является зацепление, поэтому элементы зацепления рассчитываются на прочность (по напряжениям изгиба sизг) и износ (по контактным напряжениям сжатия sсж). Кроме того, рулевые механизмы проверяются на жесткость (по величине допускаемых деформаций), а отдельные сопряжения также на удельное давление и смятие.

Рулевой механизм с глобоидальным червяком и роликом обладает высокой изгибной прочностью. Поэтому его рассчитывают по величине напряжения сжатия

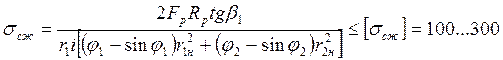 МПа,

где

Fр

– максимальное усилие, прикладываемое к рулевому колесу;

b1

– угол подъёма винтовой линии червяка (b1 = 5…10), °;

i

– число работающих гребней ролика;

,

– наружные радиусы червяка и ролика;

,

– центральные углы контактной площади;

r1

– начальный радиус червяка.

Рулевой механизм типа винт-гайка-рейка-сектор. Опыт эксплуатации показывает, что наиболее слабым звеном с точки зрения износостойкости является винтовая пара. В ряде случаев наблюдается усталостное разрушение шариков или беговых канавок. Снижением контактных напряжений можно существенно повысить работоспособность винтовой шариковой пары и улучшить КПД рулевого механизма. Поэтому рулевые механизмы рассматриваемого типа рассчитываются по напряжениям сжатия в паре шарик-поверхность канавок:

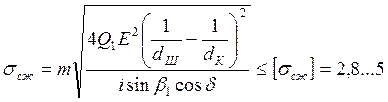 ГПа,

где

m

– коэффициент, зависящий от кривизны соприкасающихся поверхностей (m = 0,6...0,8);

Q1

– осевая сила (для расчетов принимается Q1 = 6...7 кН);

Е

– модуль упругости первого рода (Е =200), ГПа;

dШ

– диаметр циркулирующего шарика (для существующих конструкций dШ £10 мм);

dК

– диаметр канавки винта (гайки) dК = (1,03…1,04) dШ;

i

– число одновременно находящихся под нагрузкой шариков в нарезке винта (для существующих конструкций i = 22…24);

b1

– угол подъема винтовой линии винта;

d

– угол контакта шариков  (d = 45...60°).

При проектировании в первую очередь стремятся к использованию больших размеров шариков, а во вторую – к большему их количеству.

Спироидальный рулевой механизм типа цилиндрический червяк боковой сектор. Напряжение изгиба определяется для сектора, который менее прочен, чем червяк:

Скачать файл