Испытания транспортных средств: Методические указания по изучению курса и выполнению контрольной работы, страница 5

3.6. Автомобиль, динамическая характеристика которого приведена на рис. 9, двигался равномерно на прямой передаче при полном открытии дроссельной заслонки сначала на подъёме, а затем по горизонтальному участку. Оба участка дороги характеризуются одинаковой величиной коэффициента сопротивления качению.

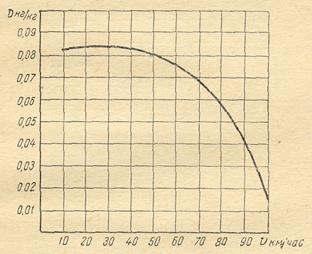
Рис. 9. Динамическая характеристика автомобиля на одной передаче

Найти величину подъёма, если известно, что после перехода на горизонтальный участок скорость автомобиля через 28 с составила υ_max = 100 км/ч. Коэффициент учёта вращающихся масс принять β = 1,07.

3.7. Используя условия задачи 3.6, найти величину подъёма, если автомобиль достиг максимальной скорости υ_max = 100 км/ч через 33 с.

3.8. Рассчитать величину пути разгона автомобиля со скорости 40 км/ч до скорости 60 км/ч, пользуясь графиком времени разгона автомобиля, приведённым на рис. 10.

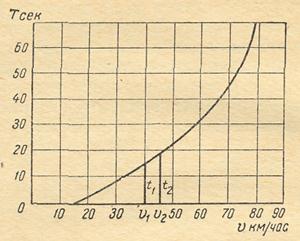
Рис. 10. График времени разгона

П р и м е ч а н и е. Приближённо путь разгона S₁ за время t₂ – t₁ при скорости 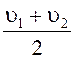будет равен:

S₁=.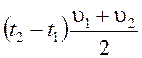

Аналогично решению задачи 3.5, интервал скоростей, в пределах которых происходит разгон автомобиля, необходимо разбить на отдельные участки с разницей в скорости 5 км/ч; затем нужно рассчитать величины пути разгона на каждом участке и, взяв суммы этих величин, определить путь разгона в заданном интервале скоростей.

3.9. Используя приведённый график на рис.11 график, определить время разгона автомобиля со скорости 20 км/ч до скорости 40 км/ч.

П р и м е ч а н и е. Время разгона в интервале скоростей υ₁ и υ₂ определяется площадью, заключённой между осью абсцисс υ, графиком  и двумя ординатами скоростей.

Переводной масштаб площади находится следующим образом: по оси абсцисс 1 мм соответствует a км/ч или  м/с; по оси ординат 1 мм соответствует b с²/м. При этом масштаб площади 1 мм² =  с.

При решении задачи принять интервалы между соседними скоростями в 5 км/ч.

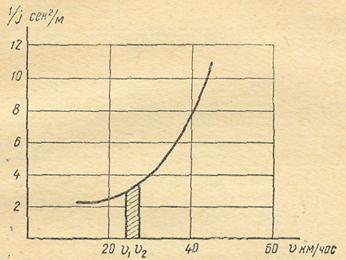
Рис. 11. График обратных ускорений в зависимости от скорости

3.10. Используя приведённый на рис. 12 график, определить путь разгона автомобиля со скорости 50 км/ч до скорости 80 км/ч.

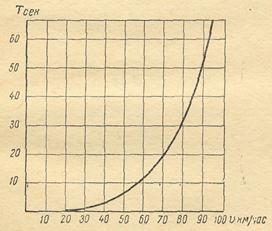
Рис. 12. График времени разгона

П р и м е ч а н и е. Путь разгона в интервале изменения времени разгона выражается в определённом масштабе площадью, заключённой между осью ординат, графиком времени разгона и горизонталями, соответствующими времени разгона в заданных интервалах скоростей.

Если 1 мм по оси абсцисс будет равен a км/ч, или  м/с, а 1 мм по оси ординат – с, тогда масштаб 1 мм² площади равен  м.

При решении задачи принять интервалы между соседними скоростями в 5 км/ч.

Задание №4. топливная экономичность автомобиля

В задании приведены задачи по определению топливной экономичности автомобиля в зависимости от степени использования мощности двигателя, скорости движения, степени использования дорожных условий. В задачах по топливной экономичности учтены экспериментальные данные испытаний автомобилей.

При решении задач этой главы следует пользоваться такими зависимостями и соотношениями

1.  Удельный расход топлива:

g_e = 1000 г/кВт·ч,

где Q – часовой расход топлива в кг/ч.

2.  Расход топлива на 100 км пути:

а) в килограммах:

Q_s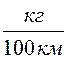 = Q_·;

б) в литрах:

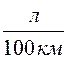Q_s = Q_s,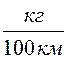

где γ – удельный вес топлива в г/см³.

3.  Расход топлива на 1 ткм:

а) в килограммах:

Q_{s = ,}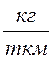

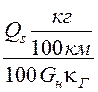где G_н – номинальная грузоподъёмность автомобиля в т;

κ_г – коэффициент использования грузоподъёмности;

б) в литрах:

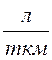Q_s = Q_s.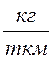

Задачи

4.1. По графику удельного расхода топлива двигателем (рис. 13) найти, сколько литров топлива израсходует автомобиль на участке в 24 км при движении на прямой передаче со скоростью 55 км/ч.

Удельный вес бензина принять γ = 0,75 г/см³. Технические данные автомобиля: передаточное число главной передачи i₀= 6,67; радиус колеса r_к = 0,44 м. Мощность двигателя при заданной скорости N_e = 70 кВт.

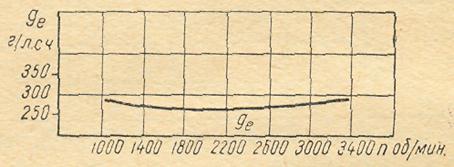
Рис. 13. График удельного расхода топлива двигателем

4.2. Используя условия задачи 4.1. определить измерение расхода топлива при движении автомобиля со скоростью 36 км/ч. Мощность двигателя при этом N_e = 50 кВт.

4.3. Используя данные, приведённые на рис. 14, определить процент использования мощности двигателя при установившемся движении автомобиля со скоростью 60 км/ч и при коэффициенте суммарного дорожного сопротивления ψ = 0,025.

______________

٭ Полная мощность, которую может развить двигатель при указанной скорости автомобиля, будет равна сумме отрезков a + b (фиг. 15), затраты мощности будут равны a + с, а процент использования мощности будет равен (a + с)/(a + b)∙100%.

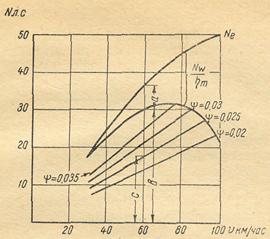
Рис. 14. Определение процента использования мощности автомобильного двигателя

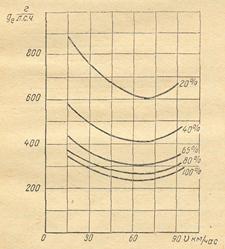
Рис. 15. Удельные расходы топлива при различных процентах использования мощности двигателя

По приведённым на рис. 15 данным определить, как возрастёт удельный расход топлива при частичном использовании мощности двигателя.

4.4. Найти соотношения процентов использования мощности двигателя и удельных расходов топлива при установившемся движении со скоростью υ = 70 км/ч по участкам дороги, характеризуемым коэффициентами суммарного дорожного сопротивления ψ₁ = 0,02 и ψ₂ = 0,035.

При решении задач воспользоваться рис. 14 и 15.

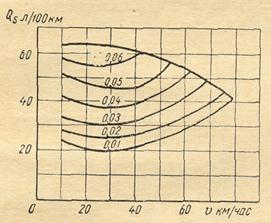
Рис. 16. Экономическая характеристика автомобиля в зависимости от величины ψ

4.5. Используя приведённую на рис. 16 экономическую характеристику полностью груженного автомобиля при установившемся его движении, найти расход топлива на пути в 121 км при следующих условиях движения на отдельных участках:

№ участка	Длина участка (в км)	Коэффициент суммарного дорожного сопротивления ψ	Время прохождения участка в минутах (t)
1	40	0,05	60
2	25	0,02	30
3	38	0,04	57
4	18	0,02	18