4.6. Определить, как изменится топливная экономичность автомобиля, экономическая характеристика которого приведена на рис. 17, при движении по дороге, характеризуемой коэффициентом суммарного дорожного сопротивления ψ = 0,03, если скорость установившегося движения будет на 50% больше, чем наиболее экономичная.
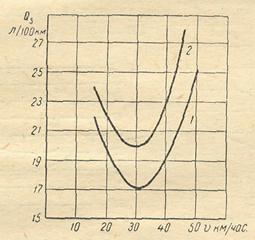
Рис. 17. Экономическая характеристика грузового автомобиля:
1 – без груза; 2 – с грузом 25000 Н
4.7. Экономическая характеристика автомобиля при движении с грузом и без груза выражена графиками на рис. 17. Автомобиль проехал с грузом и без груза по 60 км со средней скоростью движения с грузом υ = 40 км/ч и без груза υ = 50 км/ч.
Найти расход топлива на пробег с грузом и на пробег без груза.
4.8. Характеристика среднего расхода топлива грузовым автомобилем на различных дорогах и при различной полезной нагрузке выражена графиками на рис. 18.
Найти средний расход топлива Qs в л/100 км, если автомобиль 50% пути прошел по дороге 1 с грузом 1,5 т; 20% пути — по дороге 2 с грузом 2,5 т; 10% пути — по дороге 3 без груза и 20% пути — по дороге 4 с грузом 2,5 т.
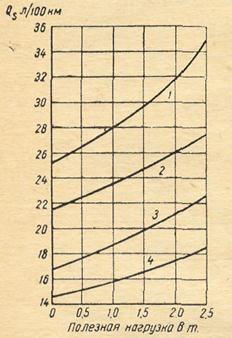
Рис. 18. Характеристика среднего расхода топлива грузовым автомобилем:
1 – грунтовая дорога; 2 – городское движение; 3 – ровное асфальтовое шоссе; холмистый рельеф; 4 – ровное асфальтовое шоссе; равнинный рельеф.
4.9. По данным испытаний понижение давления в шинах на 10% вызывает увеличение расхода топлива автомобилем на 5% по сравнению с расходом при нормальном давлении воздуха в шинах.
Определить потери топлива при указанном снижении давления в шинах за время пробега автомобиля с нагрузкой в 2,5 т на 200 км по дороге 1 (рис. 18).
Задание №5. Поворот автомобиля
В задании приведены задачи по кинематике и динамике поворота автомобиля с жёсткими и эластичными шинами.
При решении задач нужно использовать следующие соотношения и зависимости.
1. Радиус поворота автомобиля:
а) при отсутствии бокового увода шин:
R =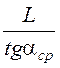
м;
б) при наличии бокового увода шин, но при постоянном угле поворота управляемых колёс aср:
R′ =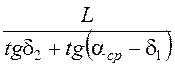
м;
где – δ1 и δ2 углы бокового увода передних и задних колёс.
Введя величины κз и κп
коэффициентов увода задней и передней осей автомобиля в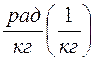 
,
можно определить радиус поворота по уравнению:
R′ =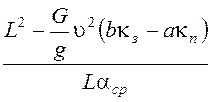
м.
2. Критическая (предельная) скорость движения автомобиля на повороте:
υкр =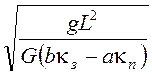 
м/с.
3. Минимальный радиус поворота автомобиля из условий бокового скольжения при равномерном движении с постоянным углом поворота:
R min=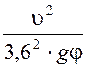
м.
4. Минимальный радиус поворота автомобиля из условий опрокидывания при равномерном движении с постоянным углом поворота:
R min = 
м.
5. Предельная скорость, до которой не будет бокового опрокидывания автомобиля дороге, без поперечного уклона, определяется по уравнению:
υ2 + mυ – n = 0,
где
m = 3,6 c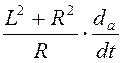
;
n = 3,62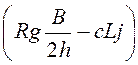
,
где с = 
;
j – ускорение в поступательном движении в м/с2;
– угловая скорость поворота управляемых колёс в 
.
Задачи
5.1. Используя приведённую на рис. 19 схему, определить как изменится величина радиуса поворота автомобиля при наличии бокового увода шин.
Технические данные автомобиля: база L = 4000 мм; средний угол поворота передних колес αср = 20°; угол увода передних колёс δ1 = 5 ◦20′; угол увода задних колёс δ2 = 3◦40′.
5.2. На какой средний угол необходимо повернуть передние управляемые колёса автомобиля при его движении со средней скоростью 54 км/ч по дороге, имеющей радиус R′ = 100 м.
Технические данные автомобиля:
вес G = 19600Н; база L = 2,8 м; расстояние по горизонтали от центра тяжести до оси ведущих колёс a = 1,3 м; коэффициент бокового увода задней оси κз = 1,810 
; коэффициент
увода передней оси Kп = 2,0·10-4
.
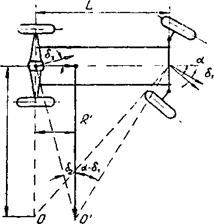
Рис. 19. Схема движения автомобиля на повороте при наличии бокового увода шин
5.3. Найти средний угол αср, на который были повернуты управляемые колеса автомобиля, двигавшегося с установившейся скоростью υ = 50 км/ч по криволинейному участку дороги с радиусом R' = 90 м.
Технические данные автомобиля:
вес G = 20000H; база L = 3 м; расстояние от центра тяжести до передней оси b = 1,8 м; коэффициент увода передней оси Kп = 2,0·10-4
; коэффициент увода задней оси
κ3 = 1,5.10-4
.
5.4. Найти величину критической (предельной) скорости устойчивого движения автомобиля на повороте.
Технические данные
автомобиля: база L = 3,5 м; расстояние по горизонтали от центра тяжести до задней оси а = 1,3 м; коэффициент бокового увода задней оси κ3 = 1,7·10-4
; коэффициент увода
передней оси κп = 2,2 · 10-4;
вес автомобиля G = 27000H.
5.5. Используя приведенную на рис. 20 схему сил, определить минимальные радиусы поворота из условий скольжения и опрокидывания.
Автомобиль движется на повороте по инерции со скоростью υ = 54 км/ч. Дорога горизонтальная, скользкая, с коэффициентом сцепления ψ = 0,3.
Технические данные автомобиля: высота центра тяжести h = 0,9 м; ширина колеи В = 1,4 м.
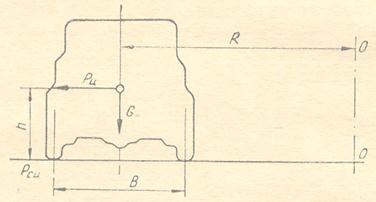
Рис. 20. Схема сил, действующих на автомобиль при движении на повороте
5.6. Автомобиль движется на повороте радиуса R = 60 м по скользкой дороге характеризуемой коэффициентом
сцепления
ψ = 0,2.
Найти предельное значение скорости, до которой автомобиль может двигаться на повороте без опасности появления бокового скольжения.
При решении задачи принять, что по условию бокового опрокидывания устойчивость автомобиля обеспечена.
5.7. Определить, что произойдет раньше: боковое скольжение или опрокидывание автомобиля и при каком минимальном радиусе поворота.
Движение происходит по инерции, на горизонтальной дороге, характеризуемой коэффициентом сцепления ψ = 0,5. Скорость движения на повороте 45 км/ч.
Технические данные
автомобиля: высота центра тяжести
h = 1,7 м; ширина колеи В = 1,5 м.
5.8. Автомобиль движется на повороте радиуса R = 40 м по горизонтальной дороге.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.