Технические данные автомобиля: расстояние по горизонтали от центра тяжести до передней оси b = 1,7 м; расстояние по горизонтали от центра тяжести до задней оси a = 1,6 м; вес, приходящийся на задние колеса, G2 = 16000H; рабочий радиус колеса rк = 0,4 м.
Решение задачи. Пользуясь схемой, составляем уравнение моментов всех сил относительно оси, соединяющей точки опоры передних колес:
Q(а – b)соs α – G[bсоs α + (h – r)sin α] = 0,
откуда
h =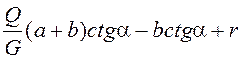 
.
Но так как
G = G2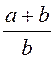
,
то после преобразования имеем:
h = b ctg α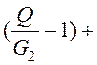
r.
Задание №3. динамика и тяговый расчёт автомобиля
В задание включены задачи, позволяющие расчётным путем определить показатели динамической характеристики автомобиля, если известны его основные конструктивные параметры. К таким показателям относятся: скорости движения на различных дорогах с различными нагрузками; величины подъемов, которые может преодолеть автомобиль в заданных дорожных условиях при движении без прицепа и с прицепом.
В этом же задании приведены задачи, решение которых позволяет оценить приемистость автомобиля, его тормозные качества, а также методы выбора основных параметров автомобиля.
При решении задач необходимо использовать следующие основные зависимости и соотношения.
1. Динамический фактор:
D =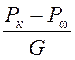 
= ƒcos α + sin α + 
ј.
2. Ускорение автомобиля:
ј =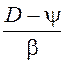 
gм/с2.
3. Баланс мощности автомобиля:
а) при равномерном движении по горизонтальному пути без прицепа:
Nеηм = Nƒ + Nw кВт;
б) то же, с прицепом:
Nеηм = Nƒ + Nw + Nкр кВт;
в) при движении автомобиля на подъём с неустановившимся режимом без прицепа:
Nеηм = Nƒ + Nw + Nj + Nh кВт;
или:
Nеηм =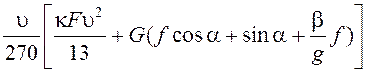 
кВт.
4. Максимальный угол подъёма, который может преодолеть автомобиль, движущийся равномерно по динамической характеристике:
sin α = D – f.
Принимается cos α
1.
5. Время движения на перегоне:
Т = 60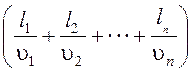
мин.
6. Максимальное значение отрицательного ускорения:
а) при торможении колёс задней оси:
Р2т max =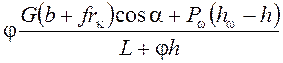 
H;
б) при торможении всех колёс:
Рт max = φ Gcos α H.
7. Максимальное значение отрицательного ускорения:
јт = 
( Рт max + f G cos α + kFυ2) м/с2.
8. Минимальный тормозной путь при действии тормозов на всех колёсах:
а) без учёта сопротивления воздуха:
Sт =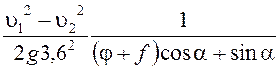 
м;
б) с учётом сопротивления воздуха:
Sт =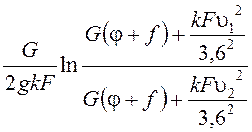 
м.
9. Минимальный тормозной путь автопоезда:
Sт =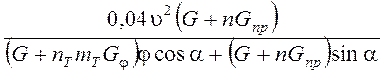 
м,
где n – число прицепов;
nт – число прицепов, имеющих тормоза;
mт – коэффициент перераспределения нагрузки для тормозящих колёс прицепа;
Gφ – сцепной вес, приходящийся на тормозящие колёса прицепа.
10. Мощность двигателя, обеспечивающая преодоление заданных сопротивлений при равномерном движении автомобиля:
Nе =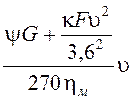 
кВт.
Задачи
3.1. Как изменится динамический фактор автомобиля при увеличении скорости с 50 до 90 км/ч на прямой передаче? При решении использовать скоростную характеристику двигателя (рис. 5).
Технические данные автомобиля: G = 1835 кг; радиус колеса
rк = 0,344 м; передаточное число главной передачи i0
= 5,125; механический к. п. д. трансмиссии ηм=
0,92; фактор сопротивления воздуха kF = 0, 076 кг·с2/м2.
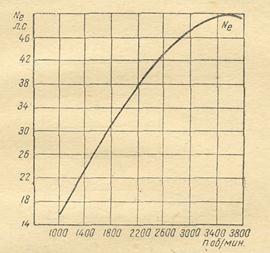
Рис. 5. Скоростная (внешняя) характеристика автомобильного двигателя
3.2. Пользуясь приведенной на рис. 5. динамической характеристикой автомобиля при различных степенях использования его грузоподъемности, найти предельную скорость движения по заданному проценту использования грузоподъёмности автомобиля и заданной дороге.
Решение задачи. Найдя на оси абсцисс точку a, показывающую заданный процент использования грузоподъемности, проводим из нее вертикаль до пересечения с наклонной линией, соответствующей заданному коэффициенту суммарного дорожного сопротивления. От полученной точки b проводим горизонталь до пересечения с кривой динамического фактора. Далее, проектируя полученную точку с на ось абсцисс, определяем значение скорости, соответствующее точке d.
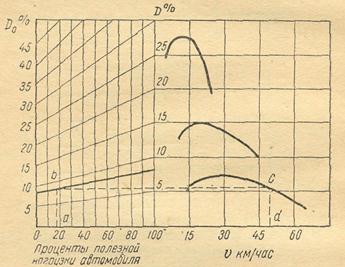
Рис. 6. Динамическая характеристика автомобиля при различных степенях использования его грузоподъемности
3.3. Найти максимальный вес груза, перевозимого автомобилем при скорости υ = 30 км/ч по дороге, характеризуемой коэффициентом суммарного дорожного сопротивления ψ = 0,08. Номинальная грузоподъемность автомобиля Gн = 25000Н.
При решении задачи использовать динамическую характеристику автомобиля (рис. 6) для условий движения на третьей передаче.
3.4. Определить максимально возможное ускорение автомобиля на четвёртой передаче при движении со скоростью υ = 45 км/ч по дороге, характеризуемой коэффициентом суммарного дорожного сопротивления ψ = 0,025.
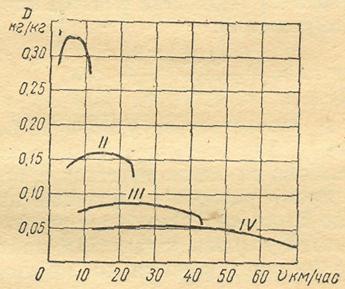
Рис. 7. Динамическая характеристика автомобиля
При решении задачи использовать динамическую характеристику автомобиля, приведённую на рис. 7.
Используя условия задачи 3.4, определить
максимально возможное ускорение при движении на второй передаче со скоростью
υ = 20 км/ч.
Коэффициент учёта вращающихся масс автомобиля принять
β1г = 1,6.
3.5. На рис. 8 приведён график ускорений автомобиля на одной передаче. Найти время разгона автомобиля со скорости υ1 км/ч до скорости υ2 км/ч.
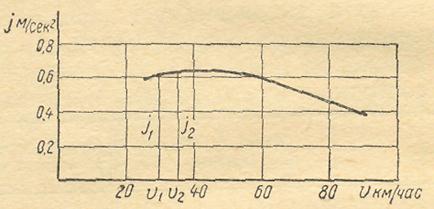
Рис. 8. График ускорений автомобиля на одной передаче
Р е ш е н и е з а д а ч и. Весь интервал скоростей, в пределах которых происходит разгон автомобиля, разбиваем на ряд отдельных участков с разницей в скорости 5 км/ч.
Время разгона на отдельном участке определяем приближённо из выражения:
t =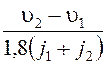 
с,
где скорости υ1 соответствует j1 ускорение, а скорости υ2 – ускорение j2. Для рассматриваемого случая определяем время разгона на шести участках и, просуммировав его, находим время разгона в заданном интервале скоростей от 30 до 60 км/ч. Оно будет равно Т = 13,3 с.
Используя условия задачи 3.5, найти время разгона автомобиля со скорости 40 км/ч до скорости 80 км/ч.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.