Зубчатый механизм. Кулачковый механизм. Структурный кинематический и кинетостатический анализ плоского рычажного механизма. Расчет маховика, страница 3

По диаграмме скоростиV_C = f(t) аналогично строим диаграмму ускоренияa_C = f(t). От начала  координат диаграммы V_C = f(t) откладываем отрезок    Op₂ = H₂ = 40 мм. Хорды поводим на участках, соответствующих   диаграмме перемещений.

    Масштаб диаграммы ускорения    

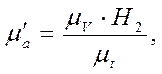                                                            (26)

                

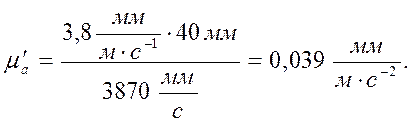
            1.6. Аналитический метод кинематического анализа

     1.6.1. Исходные данные

   Угловая скорость кривошипа: ω₁ = 135 рад/с.

   Длины звеньев АВ и АD: l_AB = l_AD = 0,09 м.

   Длины звеньев BCи DE: l_BC = l_DE = 0,32 м.

   Центр масс звеньев BCи DE: l_BS2 = l_DS4 = 0,3 l_BC = 0,096 м.

   Угол поворота кривошипа: φ₁ = 30˚ … 360˚, 30˚.

     1.6.2. Алгоритм расчета

Расчетная схема кинематической цепи приведена на рис. 5.

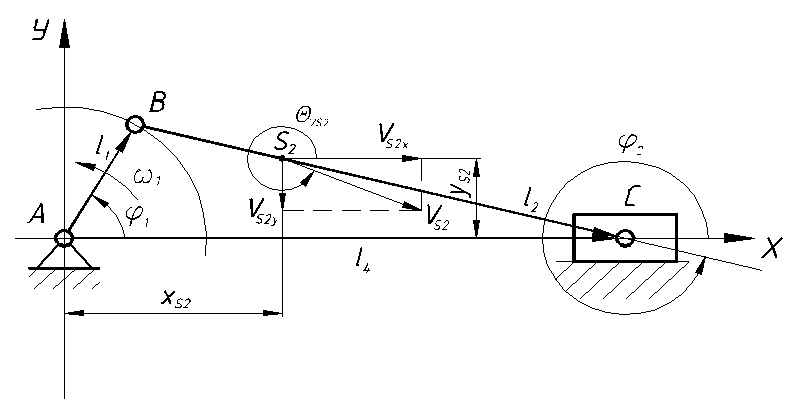
      Рисунок 7 - Расчетная схема.

Векторное уравнение по методу замкнутых векторных контуров имеет вид:

                                                                 (27)

где l₁ = l_AB  - длина кривошипа;

l₂ = l_BC- длина шатуна.

Направляющий угол   φ₂ вектора l₂ определяется по зависимости:

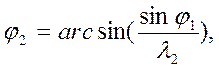                                                   (28)

где  φ₂  - угол расположения начального звена 1;

λ₂- относительная длина звена 2.

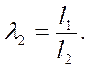                  (29)

Направляющие углы по величине определяются как углы между положительным направлением оси X  и вектором в направлении против часовой стрелки.

   Угловая скорость шатуна:   

     (30)

Угловое ускорение шатуна:

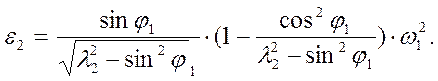                               (31)

   Положительные значения угловых параметров и соответствуют их направлению против часовой стрелки, отрицательные - по часовой стрелке.

Линейная координата точки С ползуна, отсчитывается от точки А:

        (32)

Расстояние от левой (нижней) мертвой точки до ползуна:

                                                             (33)

Дифференцирование выражения 32 дает скорость ползуна: 

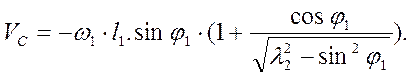       (34)

Повторное дифференцирование дает ускорение ползуна:

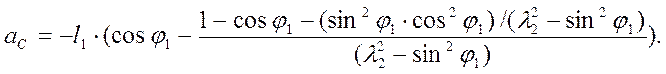   (35)

Положение центра масс шатуна   определятся линейными координатами:

      (36)

                      (37)

где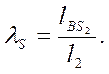

При дифференцировании уравнений 36 и 37 получается выражение для определения проекций скоростей на координатные оси:

             (38)

             (39)

Полная скорость:

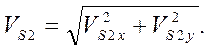                       (40)

Ее направление определяется с учетом угла 

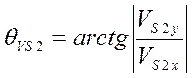                         .                               (41)

Величина угла направления скорости центра масс шатуна зависит от знака проекций скоростей и определяется из таблицы 1.1.

 Таблица 1.1

В результате дифференцирования уравнений 38, 39 получаются ускорения:

        (42)

          (43)

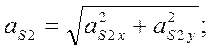                                                         (44)

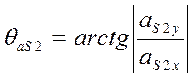                               .                            (45)

Направление вектора   определяется аналогично углу  (см. табл. 1.1)

Линейная скорость точки В:

                                                                 (46)

Линейное ускорение точки В :

                                                                 (47)

Кинематическая цепь ADE с теми же размерами элементов, что и для цепи ABC, будет иметь следующие значения соответствующих параметров движения в каждый момент времени:

      1.6.3. Распечатка машинных данных

   Таблица 1.2 – Угловые параметры шатуна

n	φ2 , град	ω2 , рад/с	ε2 , рад/с2
3	0	-38,0	0
2	-8,1	-33,2	2432
1	-14,1	-19,6	4480
12	-16,3	0	5341
11	-14,1	19,6	4480
10	-8,1	33,2	2430
9	0	38,0	0
8	8,1	33,2	-2432
7	14,1	19,6	-4480
6	16,3	0	-5341
5	14,1	-19,6	-4480
4	8,1	-33,2	-2432