Лекция №14
14.8. Расчёт по контактным напряжениям
Расчёты на прочность цилиндрических зубчатых передач стандартизированы по ГОСТ 21345. Задача расчёта состоит в определении таких значений основных параметров передачи, которые наилучшим образом удовлетворяют прочностным, триботехническим, кинематическим, геометрическим и экономическим требованиям.
Исследованиями установлено, что наименьшей контактной усталостной прочностью обладает околополюсная зона рабочей поверхности зубьев. Поэтому расчёт контактных напряжений принято выполнять при контакте в полюсе зацепления (рис. 14.18).
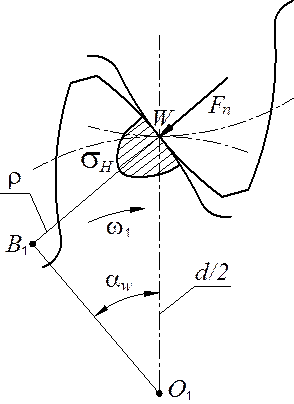 |
Рис. 14.18. Контактные напряжения в зацеплении
Контакт зубьев можно
рассматривать как контакт двух цилиндров с радиусами ![]() и
и
![]() . При этом контактные напряжения определяют
по формуле Герца – формула (2.30):
. При этом контактные напряжения определяют
по формуле Герца – формула (2.30):
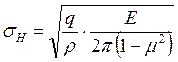 .
(14.28)
.
(14.28)
Удельную нагрузку определяют по формуле:
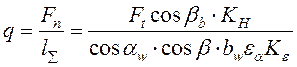 , (14.29)
, (14.29)
где ![]() –
коэффициент, учитывающий неравномерность распределения нагрузки по длине
контактной линии;
–
коэффициент, учитывающий неравномерность распределения нагрузки по длине
контактной линии; ![]() = 0,95 для косозубых колес;
= 0,95 для косозубых колес;
![]() –
коэффициент нагрузки при расчёте по контактным напряжениям;
–
коэффициент нагрузки при расчёте по контактным напряжениям;
![]() ,
(14.30)
,
(14.30)
![]() –
коэффициент, учитывающий неравномерное распределение нагрузки между несколькими
зацеплениями (в косозубой передаче).
–
коэффициент, учитывающий неравномерное распределение нагрузки между несколькими
зацеплениями (в косозубой передаче).
Радиус кривизны эвольвенты в полюсе зацепления:
![]() .
(14.31)
.
(14.31)
С учетом эквивалентного диаметра (п. 14.2) радиус кривизны
![]() .
.
Приведенная кривизна:
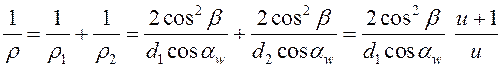 . (14.32)
. (14.32)
С учетом (14.31) и (14.32) формула Герца примет вид:
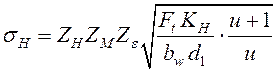 , (14.33)
, (14.33)
где ![]() – коэффициент, учитывающий форму
сопряжённых поверхностей;
– коэффициент, учитывающий форму
сопряжённых поверхностей;
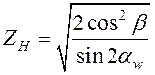 ; (14.34)
; (14.34)
![]() –
коэффициент, учитывающий механические свойства материалов колёс;
–
коэффициент, учитывающий механические свойства материалов колёс;
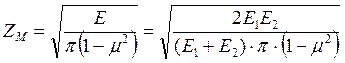 ; (14.35)
; (14.35)
![]() –
коэффициент, учитывающий суммарную длину контактных
линий;
–
коэффициент, учитывающий суммарную длину контактных
линий;
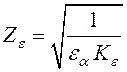 .
(14.36)
.
(14.36)
Формулу (14.33) можно
видоизменить и упростить, приняв стальные колёса с ![]() 2,15×105 МПа и μ = 0,3, коэффициент перекрытия
2,15×105 МПа и μ = 0,3, коэффициент перекрытия ![]() 1,8, коэффициент
1,8, коэффициент ![]() 0,95,
угол зацепления
0,95,
угол зацепления ![]() 20º, а параметры
20º, а параметры ![]() и
и ![]() записать
с учётом геометрических соотношений:
записать
с учётом геометрических соотношений:
![]() ;
; 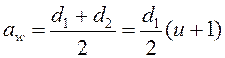 ,
откуда
,
откуда 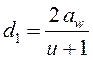 , (14.37)
, (14.37)
![]() . (14.38)
. (14.38)
После упрощений формула проверочного расчёта примет вид:
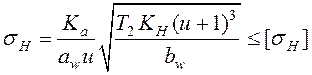 . (14.39)
. (14.39)
где ![]() –
численный коэффициент, равный 270 для косозубых и шевронных колес и 315 – для
прямозубых; величина коэффициента соответствует единицам измерения Ньютон и
миллиметр, то есть Т2 в Н×мм, bw в мм, sН в МПа (Н/мм2).
–
численный коэффициент, равный 270 для косозубых и шевронных колес и 315 – для
прямозубых; величина коэффициента соответствует единицам измерения Ньютон и
миллиметр, то есть Т2 в Н×мм, bw в мм, sН в МПа (Н/мм2).
Формула (14.39) не пригодна
для проектного расчета, так как содержит два неизвестных геометрических
параметра ![]() и b. Для дальнейшего упрощения решения задачи один
параметр выражают через другой. Вводят коэффициент ширины колеса
и b. Для дальнейшего упрощения решения задачи один
параметр выражают через другой. Вводят коэффициент ширины колеса
![]() , откуда
, откуда ![]() .
(14.40)
.
(14.40)
Коэффициент ![]() для косозубых колес принимают
для косозубых колес принимают ![]() = 0,2…0,5. Подставляя (14.40) в формулу
(14.39) и решая её относительно
= 0,2…0,5. Подставляя (14.40) в формулу
(14.39) и решая её относительно ![]() , получают формулу
проектного расчёта:
, получают формулу
проектного расчёта:
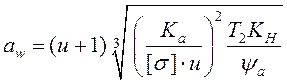 . (14.41)
. (14.41)
Вычисленное значение ![]() округляют до ближайшего значения либо по
ГОСТ 2185, либо из ряда Ra40 ГОСТ
6636 (Прил. 15). Остальные геометрические параметры определяют в результате
расчёта геометрии. В дальнейшем определяют окружную скорость, уточняют
коэффициенты нагрузки, определяют силы в зацеплении и выполняют проверку
контактных и изгибных напряжений. При расчёте внутреннего зацепления
в формулах (14.39) и (14.41) ставят (u -
1) вместо (u + 1).
округляют до ближайшего значения либо по
ГОСТ 2185, либо из ряда Ra40 ГОСТ
6636 (Прил. 15). Остальные геометрические параметры определяют в результате
расчёта геометрии. В дальнейшем определяют окружную скорость, уточняют
коэффициенты нагрузки, определяют силы в зацеплении и выполняют проверку
контактных и изгибных напряжений. При расчёте внутреннего зацепления
в формулах (14.39) и (14.41) ставят (u -
1) вместо (u + 1).
В реечной передаче должны быть известны: Ft - окружная сила на шестерне, v – скорость рейки. Делительный диаметр из расчёта на контактную выносливость:
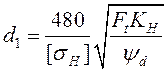 .
(14.42)
.
(14.42)
Рекомендуется коэффициент
ширины ![]() = b/d1 = 0,4…0,8. Предварительное значение модуля:
= b/d1 = 0,4…0,8. Предварительное значение модуля:
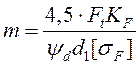 .
(14.43)
.
(14.43)
Число зубьев шестерни
реечной передачи z1 = d1/m ![]() 12. После округления модуля и
числа зубьев уточняют диаметр шестерни: d1 = mz1.
12. После округления модуля и
числа зубьев уточняют диаметр шестерни: d1 = mz1.
14.9. Расчёт по изгибным напряжениям
Расчётная схема
представлена на рис. 14.19. Зуб рассматривают как консольную балку, нагруженную
нормальной силой ![]() , которая приложена к кромке зуба
(наиболее неблагоприятный случай). Предпосылки расчёта:
, которая приложена к кромке зуба
(наиболее неблагоприятный случай). Предпосылки расчёта:
1) Вся нагрузка
прямозубого зацепления передается одной парой зубьев и приложена к вершине
зуба. Нормальная сила будет в этом случае располагаться не под углом зацепления
![]() , а под углом давления
, а под углом давления ![]() 28…30° для прямозубой передачи.
28…30° для прямозубой передачи.
2) Влиянием сил трения пренебрегают ввиду их малости.
3) Зуб рассматривают как консольную балку, для которой справедлива гипотеза плоских сечений, следовательно, методы сопротивления материалов.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.