1. Функція f строго зростає (зростає) на множині Х:
Якщо
![]() , то
, то ![]() .
.
2. Функція f зростає (не спадає) на множині Х:
Якщо
![]() , то
, то ![]() .
.
3. Функція f строго спадає (спадає) на множині Х:
Якщо
![]() , то
, то ![]() .
.
4. Функція f спадає (не зростає) на множині Х:
Якщо
![]() , то
, то ![]() .
.
Основні функції
1. Лінійна функція
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Функція строго зростає при a>0 строго спадає при a<0.
Графік функції - пряма лінія.
2. Квадратична функція
![]() ,
,
![]() :
:
а) a>0
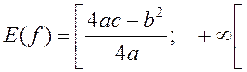 .
.
Функція
строго спадає на проміжку 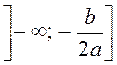 і строго зростає на
проміжку
і строго зростає на
проміжку 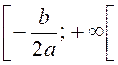 .
.
Графік
функції – парабола з віссю 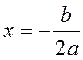 , вершиною в точці
, вершиною в точці 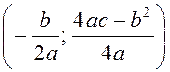 і вітками, спрямованими угору;
і вітками, спрямованими угору;
б) a>0
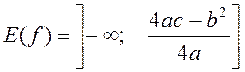 .
.
Функція
строго зростає на проміжку 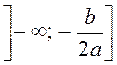 і строго спадає на
проміжку
і строго спадає на
проміжку 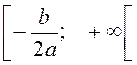 .
.
Графік
функції – парабола с віссю 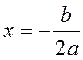 , вершиною в точці
, вершиною в точці 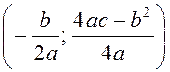 і вітками, спрямованими вниз;
і вітками, спрямованими вниз;
3. Степенева функція
![]() :
:
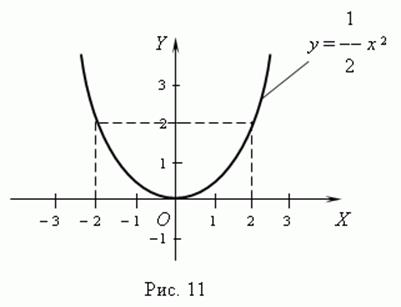
а) ![]() (рис.1 ),
(рис.1 ),
|
![]() ,
,
![]() ,
,
![]() .
.
Функція
парна, строго спадає на проміжку ![]() , строго зростає на
проміжку
, строго зростає на
проміжку ![]() ;
;
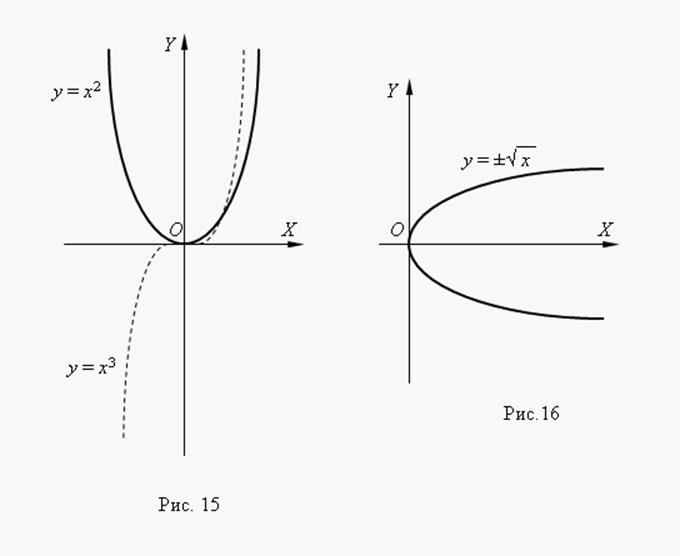
б) ![]() (рис.2),
(рис.2),
|

![]() ,
,
![]() ,
,
![]() .
.
Функція непарна, строго зростає;
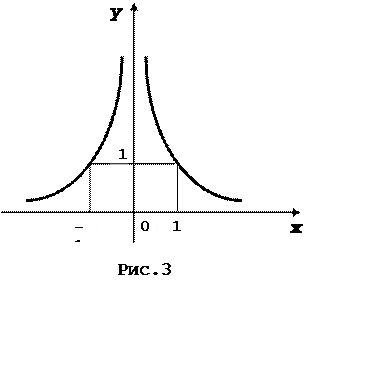
в) ![]() (рис.3),
(рис.3),
 |
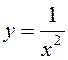
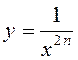 ,
,
![]() ,
,
![]() .
.
Функція
парна, строго зростає на проміжку ![]() , строго спадає на
проміжку
, строго спадає на
проміжку ![]() ;
;
г) ![]() (рис.4)
(рис.4)
|
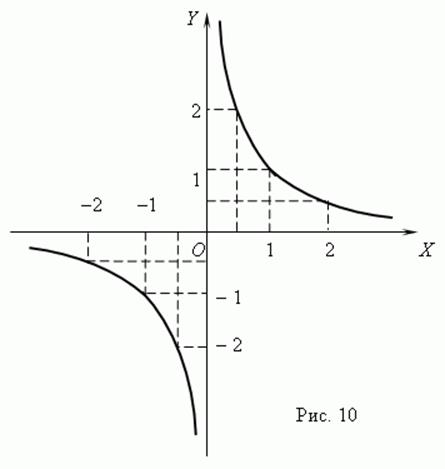
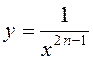 ,
,
![]() ,
,
![]() .
.
Функція
непарна, строго спадає на проміжку ![]() і
і ![]() .
.
Показникова функція (рис.5)
|
|
|
|
|
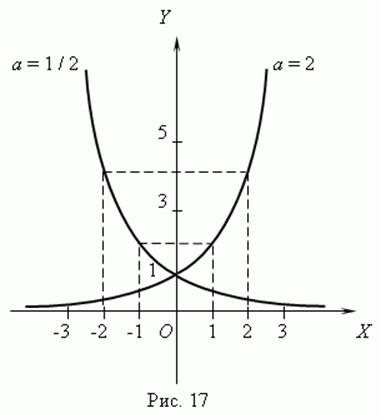
![]() ,
,
![]() ,
,
![]() .
.
При 0<a<1 функція строго спадає, при a>1 – строго зростає.
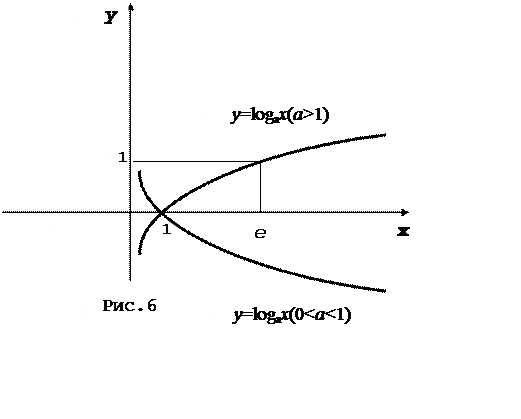
4. Логарифмічна функція
(рис.6)
 |
|||
![]() ,
,
![]() ,
,
![]() .
.
Функція строго зростає.
Логарифм з основою а
![]() ,
,
![]() ,
,
![]() .
.
При 0<a<1 функція строго спадає, при a>1 – строго зростає.
5. Тригонометричні функції
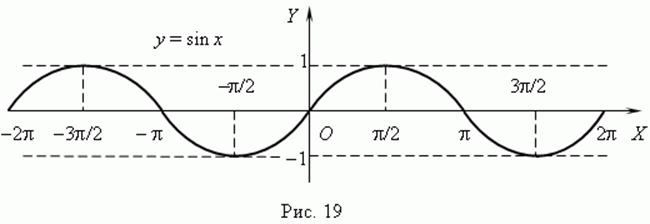
а) ![]() (рис.7),
(рис.7),
|
|
![]() ,
,
![]() .
.
Функція непарна.
Період ω=2p.
На кожному з проміжків 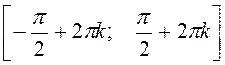 ,
, ![]() функція строго зростає, на
функція строго зростає, на 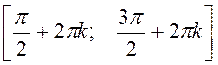 ,
, ![]() –
функція строго спадає;
–
функція строго спадає;
б) y=cosx (рис.8),
|
|

![]() ,
,
![]() .
.
Функція парна.
Період ω=2p.
На кожному з проміжків ![]() ,
, ![]() функція
строго спадає, на
функція
строго спадає, на ![]() ,
, ![]() –
строго зростає;
–
строго зростає;
в) y=tgx(рис.9),
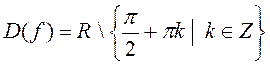 ,
,
![]() .
.
Функція непарна.
Період ω=p.
Функція
строго зростає на кожному з проміжків 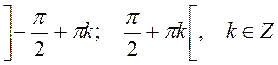 ;
;
г) y=сtgx (рис.9),
![]() ,
,
![]() .
.
|
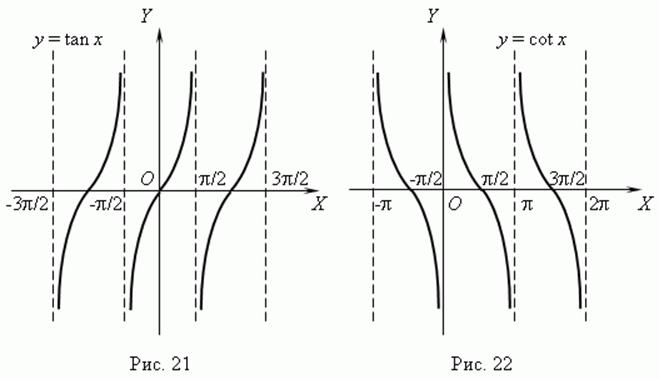
Функція непарна,
Період ω=p.
Функція строго спадає на кожному з проміжків
![]()
6. Обернені тригонометричні функції
а) y=arcsinx (рис.10),
![]() ,
,
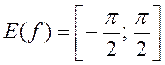 .
.
|
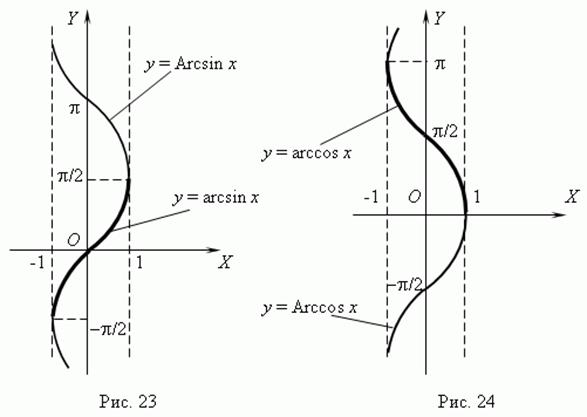
Функція непарна, строго зростає.
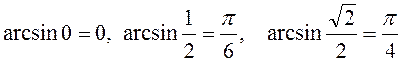 ,
,
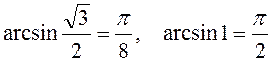 ;
;
б) y=arccosx (рис.10),
![]() ,
,
![]() .
.
Функція строго спадає.
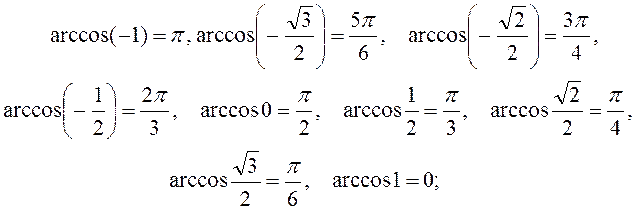
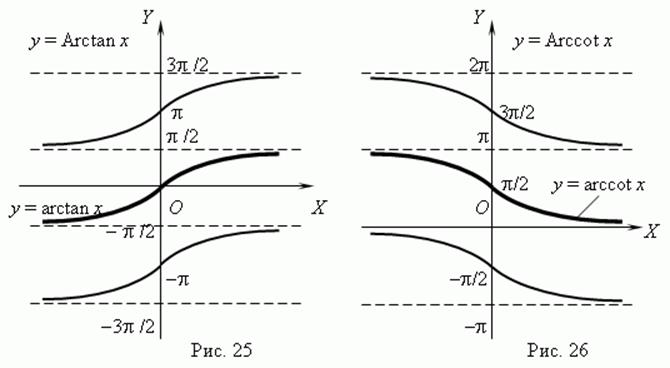
в) y=arctgx (рис.11),
![]() ,
,
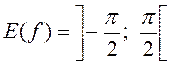 .
.
Функція непарна строго зростає.
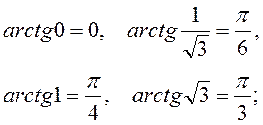
г) y=arcсtgx (рис.11),
![]() ,
,
![]() .
.
Функція строго спадає.
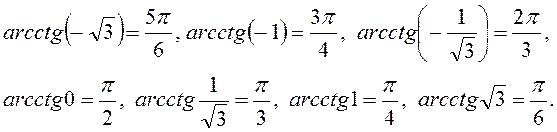
|
Геометрія
Довжина кола
![]() .
.
Площі
Трикутник: 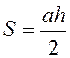 (а – основа, h - висота);
(а – основа, h - висота);
![]() - (р
– півпериметр, a,bic –
сторони);
- (р
– півпериметр, a,bic –
сторони); 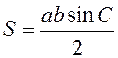 .
.
Для рівнобічного трикутника 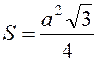 - (a – сторона
трикутника).
- (a – сторона
трикутника).
Паралелограм: ![]() (b –
основа, h - висота).
(b –
основа, h - висота).
Ромб:  (d1 і d2 –
діагоналі).
(d1 і d2 –
діагоналі).
Трапеція: 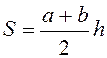 (а і b –
основи, h - висота).
(а і b –
основи, h - висота).
Коло: ![]() .
.
Поверхні
Призма: Sбок=Рl (Р –периметр перпендикулярного перетину, l– бічне ребро).
Правильна піраміда: 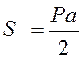 (Р
–периметр основи, a - апофема).
(Р
–периметр основи, a - апофема).
Циліндр: Sбок.= 2pRH.
Конус: Sбок.= pRl (l – твірна).
Куля: S =4pR2.
Об’єми
Призма: V=S×H (S –площа основи, H– висота).
Піраміда: 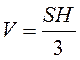 .
.
Циліндр: V =pR2H.
Конус: 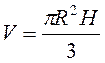 .
.
Куля: 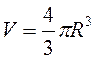 .
.
Співвідношення між елементами прямокутного трикутника
(a, b – катети; с – гіпотенуза; А, В – гострі кути; С – прямий)
1. a= с sinА= с cosВ.
2. b= с sinВ= с cos А.
3. a=btgА= bctgВ.
4. b= atgВ= actg А.
Співвідношення між елементами довільного трикутника
(a, b, с – сторони; А, В, С -кути)
1. 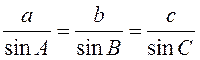 (теорема
синусів).
(теорема
синусів).
2. ![]() (теорема
косинусів).
(теорема
косинусів).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.