Розв¢язання.
Нехай перший магазин перевозив кавуни порціями по х тон в день, а другий – по у тон в день. Нехай процес перевезення від самого початку тривав zднів. За умовою задачі магазини отримали однакову кількість кавунів, причому другий магазин вивозив кавуни z – а днів, тому
z× х =( z – а )×у. (1)
Розглянемо два випадки.
1) 
Тоді саме перший
магазин за b днів перевіз
половину усіх кавунів, тобто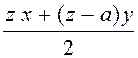 
,
що, з іншого боку, дорівнює bx.
Маємо рівняння:
.
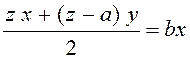З урахуванням (1):
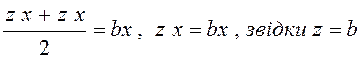( так як за умовою
х>0), що неможливо, бо означає, що другий
магазин взагалі не буде перевозити кавуни, а це суперечить умові задачі.
2) b > a
За b днів перший магазин перевіз bх тон кавунів, а другий магазин ( b – a)y тон кавунів, що є половиною усіх кавунів, вивезених з бази. Тоді
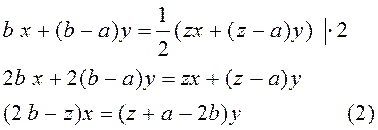
З рівняння (1):
.
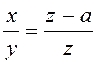З рівняння (2):
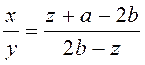
інакше з (2) одержуємо, що а = 0 або у =
0, що суперечить умові задачі).
Тоді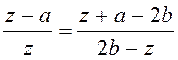 
- розв¢яжемо
це рівняння.
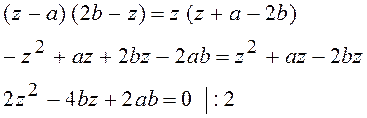
, так як b
> a.
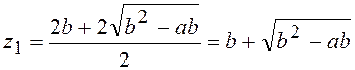
- не
підходить, тому що z > b.
Отже,
кавуни були перевезені за 
днів.
Відповідь: 
ЗАВДАННЯ ДЛЯ САМОКОНТРОЛЮ ЗА ОСНОВНИМИ ТЕМАМИ
ШКІЛЬНОЇ МАТЕМАТИКИ
Натуральні числа, дії над ними.
Подільність натуральних чисел. Прості та складені числа. Найбільший спільний, найменше спільне кратне.
1. Знайти дільники чисел:
132, 448, 700, 56785, 1200, 1062, 15189, 3141, 5796, 11250, 34875
2. Знайти кратні до чисел 67, 98, 34, 67, 53.
3. Знайти найменше спільне кратне до чисел
- 24 та 36;
- 23, 45, 69;
- 8, 56, 6, 48.
- 33, 99, 121.
4. Знайти найбільший спільний дільник до чисел
- 72, 18.
- 121, 187, 253.
- 45, 135, 315.
5. Знайти НСД та НСК чисел 126, 540, 630, 144, 1008, 1224.
6. Число 19 представити у вигляді різниці кубів натуральних чисел. Показати, що це представлення єдине.
7. Розкласти на множники числа
642, 936, 71421, 876, 534680, 456.
8. Далі самостійно візьміть будь-які числа та спробуйте розкласти на множники.
Звичайні дроби та дії над ними. Правильний та неправильний дріб. Основна властивість дробу. Скорочення дробу. Середнє арифметичне кількох чисел
1. Порівняйте дроби за величиною
2. а) 11/14 та 8/14;
3. б) 7/13 та 7/14;
4. в) 3/14 та 5/21.
5. Оберніть десяткові дроби у звичайні дроби: 0,5; 1,7; 3,75; 25,04; 0,08.
6. Оберніть звичайні дроби у десяткові дроби: 3/5; 7/8; 3/15; 11/4; 31/2; 4/7; 2/9.
7.
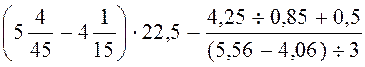
8.
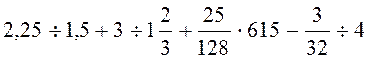
9.
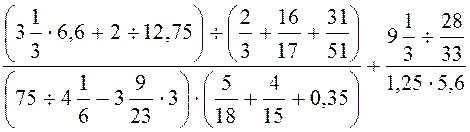
10.
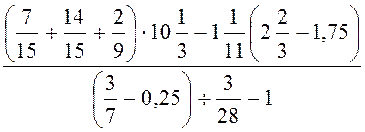
11.
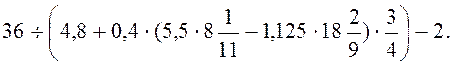
12.
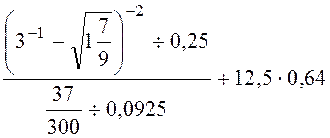
13.Знайти Х з пропорції
14.
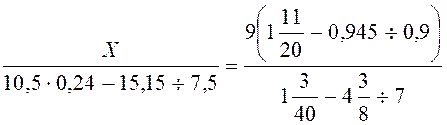
15.
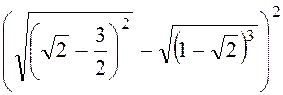
16. 
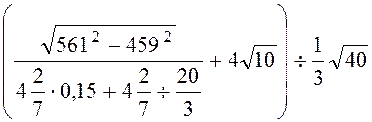
Пропорції. Відсоток. Основні задачі на відсотки
1. Поділити число 180 на дві частини таким чином, щоб 4% першої частини та 6% другої складали разом число, щоб дорівнювало б 4,5 % усього числа.
2. Кілограм товару коштував 6,4 у.г.о. Після зниження ціни він коштував 5,44 у.г.о. Наскільки процентів була знижена ціна на товар?
3. Поділити число 175 на частини пропорційно кубам чисел 2 і 3.
4. Морська вода містить 5% солі. Скільки кілограмів прісної води треба додати до 40 кг морської, щоб в останній було 2 % солі?
5. Маса сплаву 67 кг, і він складається з срібла й міді, причому маса срібла складає 34% маси міді. Скільки срібла у сплаві?
6. Скільки води треба випарити з 988 кг маси, яка містить 85% води, щоб одержати масу з 48% води.
7. Свіжі фрукти містять 72% води, а сухі 20%. Скільки сухих фруктів виходить з 20 кг свіжих?
8. Свіжі гриби містять 90% води, сухі 12% води. Скільки виходить сухих грибів із 44 кг свіжих?
Степінь з натуральним і раціональним показником. Арифметичний корінь n-го степеня та його властивості
1. Що більше: а 452 –312 або 442 – 302;
б) 297*299 або 2982;
в) 263 – 243 або (26-24)3;
г) (17+13)3 або 173 +133.
2. Знайдіть значеня виразу:
а)
;
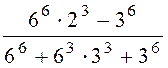б)
.
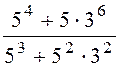3. Обчислити
а)
;
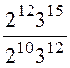б)
;
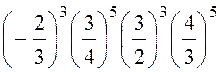в)
;
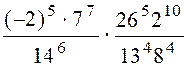г)
;
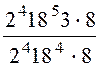д)
.
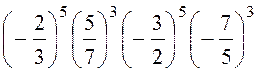4. Позбавитись
від ірраціональності у знаменнику а)
; б)
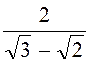; в)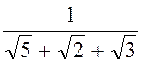 
5. Винести
з під знаку кореня а)
;
б)
;
в)
.
6. Внести
під знак кореня а)
;
б)
;
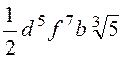7. Спростити
а)
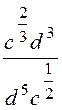; г)
;
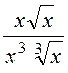Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.