6.
Вектори ![]() і
і ![]() утворюють кут j = 120°, причому |
утворюють кут j = 120°, причому |![]() |=3 і |
|=3 і |![]() |=5. Визначити |
|=5. Визначити |![]() | та |
| та |![]() |.
|.
7.
Якій умові повинні задовольняти вектори ![]() і
і ![]() щоб мали місце такі співвідношення:
щоб мали місце такі співвідношення:
1)|![]() |=|
|=|![]() |; 2)|
|; 2)|![]() |>|
|>|![]() |; 3)
|; 3)![]()
8.
Якій умові повинні задовольняти вектори ![]() і
і ![]() , щоб вектор
, щоб вектор
![]() ділив навпіл кут між векторами
ділив навпіл кут між векторами ![]() і
і ![]() .
.
9.
За даними векторами ![]() і
і ![]() побудувати такі вектори:
побудувати такі вектори:
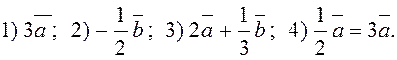
10. Точка О є центром ваги трикутника АВС. Довести, що
![]()
11.
Перевірити колінеарність векторів ![]() ={2; -1; 3} і
={2; -1; 3} і ![]() {-6; 3; -9}. Визначити, який з них довше і у скільки разів, як
вони направлені- в один бік чи в протилежні сторони.
{-6; 3; -9}. Визначити, який з них довше і у скільки разів, як
вони направлені- в один бік чи в протилежні сторони.
12.
Визначити,при яких значеннях a,b вектори ![]() =-2i+3j+bk та
=-2i+3j+bk та ![]() =ai-6j+2k
колінеарні.
=ai-6j+2k
колінеарні.
13. Перевірити та впевнитись, що чотири точки А(3; -1; 2),В(1; 2;-1), С(-1;1;-3), D(5;0;4) служать вершинами трапеції.
14. Маємо точки А(-1; 5; -10), В(5; -7; 8), С(2; 2; -7) та D(5; -4;2).
Перевірити
і впевнитись, що вектори ![]() та
та ![]() колінеарні; встановити який з них довше і
у скільки разів, як вони направлені- в один бік чи в протилежні сторони.
колінеарні; встановити який з них довше і
у скільки разів, як вони направлені- в один бік чи в протилежні сторони.
15. Маємо дві вершини А(2; -3;-5), В(-1;3; 2) паралелограма АВСD і точка перетину його діагоналей Е(4; -1; 7).Визначити дві інші вершини цього паралелограма.
Геометрія
1. Із точки А, яка не лежить на колі, проведені до неї дотична і січна. Відстань від точки А до точки дотику дорівнює 16 см, а відстань від точки А до однієї з точок перетину січної з колом дорівнює 32 см. Знайти радіус кола, якщо січна віддалена від центра на 5 см.
2.
Основа
рівнобедреного трикутника дорівнює ![]() см, а медіана бічної
сторони дорівнює 5 см. Знайти бічну сторону.
см, а медіана бічної
сторони дорівнює 5 см. Знайти бічну сторону.
3. Сума довжин діагоналей ромба дорівнює m, а його площа дорівнює S. Знайти сторону ромба .
4. Плоский кут при вершині правильної трикутної піраміди дорівнює 900. Знайти відношення бічної поверхні цієї піраміди до площі її основи.
5. У прямому паралелепіпеді сторони основи дорівнюють а і b, гострий кут між ними дорівнює 600. Більша діагональ основи дорівнює меншій діагоналі паралелепіпеда. Знайти об¢єм паралелепіпеда.
6. Знайти довжину твірної конуса, нахиленої до площі основи під кутом a, якщо вписана в нього правильна трикутна призма, основа якої лежить у площині основи конуса, має ребра в основі довжиною а і бічні ребра довжиною 2а.
7. Усередині прямого кута дана точка М, відстані якої від сторін кута дорівнюють 4 см і 8 см. Пряма, що проходить через точку М, відсікає від прямого кута трикутник з площею 100 см2. Знайти катети трикутника.
8. Основи трапеції дорівнюють 4 см і 16 см. Знайти радіуси кіл, вписаного і описаного навколо неї, якщо відомо, що ці кола існують.
9. Вершини прямокутника, вписаного в коло, поділяють його на чотири дуги. Знайти відстані від середини однієї з більших дуг до вершини прямокутника, якщо сторони його дорівнюють 24 см і 7 см.
10. Основою паралелепіпеда служить ромб зі стороною а і гострим кутом 300. Діагональ однієї бічної грані перпендикулярна до площі основи, а бічне ребро складає з площиною основи кут 600. Знайти повну поверхню і об¢єм паралелепіпеда.
11. Кут між твірною
конуса і площиною основи дорівнює 300. Бічна поверхня конуса
дорівнює ![]() см. Визначити об¢єм правильної
шестикутної піраміди, вписаної в цей конус.
см. Визначити об¢єм правильної
шестикутної піраміди, вписаної в цей конус.
ОСНОВНІ ФОРМУЛИ ШКІЛЬНОЇ МАТЕМАТИКИ
Алгебра
Дії із степенями
1. ![]() .
.
2. 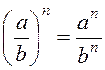 .
.
3. am ·аn =am + n.
4. am : an =am - n;.
5. 1: an= a-n.
6. (a m ) n = am n.
Дії з коренями
1. ![]() .
.
2. 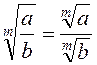 .
.
3. 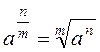 .
.
4. ![]() .
.
Квадратні рівняння
ax²+bx+c=0; (a¹0)
x1,2= (-b±ÖD)/2a; D=b²– 4ac
D>0® x1¹x2 ;D=0® x1=x2
D<0, коренів немає.
Теорема Вієта: x² + px+q =0
x1+x2 = -p, x1×x2 = q.
Якщо p=2k (p-парне) та x²+2kx+q=0, то x1,2 = -k±Ö(k²-q).
Прогресії
Формули арифметичної прогресії
![]() ;
;
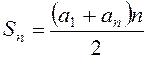 ;
;
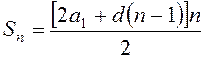 .
.
Формули геометричної прогресії
![]() ;
;
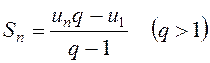 ;
;
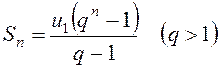 ;
;
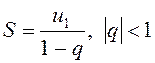 (нескінченна спадна геометрична
прогресія).
(нескінченна спадна геометрична
прогресія).
Формули скороченого множення і розкладання на множники
(a±b)²=a²±2ab+b²;
(a±b)³=a³±3a²b+3ab²±b³;
a²-b²=(a+b)(a-b);
a³±b³=(a±b)(a²‡ab+b²);
ax²+bx+c=a(x-x1)(x-x2), где x1 и x2 – корені рівняння ax²+bx+c=0.
Логарифми
1. ![]() ;
;
2. ![]() ;
;
3. ![]() ;
;
4. ![]() ;
;
5. 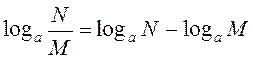 ;
;
6. ![]() ;
;
7. 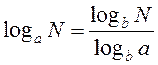 .
.
Тригонометрія
sin² a + cos² a =1;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.