Збірник завдань для контролю вхідного рівня знань з математики, страница 7

tg a = cosa / sina , a¹pn, nÎZ:

tga × ctga = 1, a ¹ (pn)/2, nÎZ;

1+tg²a = 1/cos²a , a¹p(2n+1)/2;

1+ ctg²a =1/sin²a , a¹pn.

Формули складання

1. sin (α ±  β) = sin α cos β ± cos α sin β;

2. cos (α ± β) = cos α cos β ± sin α sin β;

3. .

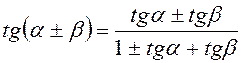Знаки тригонометричних функцій по чвертям

Значення тригонометричних функцій деяких кутів

Функція Кути 0° 30° 45° 60° 90° 180° 270° 360° Градуси 0° Радіани sin α 0 1 0 –1 0 cos α 1 0 –1 0 1 tg α 0 1 – 0 – 0 ctg α – 1 0 – 0 –

Формулизведення

sin α –sin α sin α sin α –sin α cos α cos α –cos α –cos α cos α –cos α –cos α cos α cos α –sin α sin α sin α –sin α tg α tg α –tg α tg α –tg α –ctg α ctg α –ctg α ctg α ctg α ctg α –ctg α ctg α –ctg α –tg α tg α –tg α tg α

Співвідношення між тригонометричними функціями

;

.

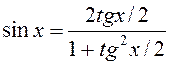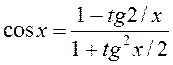Тригонометричні рівняння

sinx = m ; |m| ≤ 1

x = (-1)ⁿ arcsin m + pk, sin x =1,    x = p/2 + 2pk.

Окремі випадки:

sin x= 0,     x = pk,

sin x = -1,   x = -p/2 + 2 pk,

cos x = m; |m| ≤ 1,

x = ± arccos m + 2pk,    kÎ Z.

Окремі випадки:

cos x = 1,    x = 2pk,

cos x = 0,      x = p/2+pk,

cos x = -1,        x = p+ 2pk.

tg x = m

x = arctg m + pk.

ctg x = m

x = arcctg m +pk.

Подвійні і половинні кути

1. sin 2α =2 sin α cosα;

2. cos2α= cos² α – sin² α;

3. ;

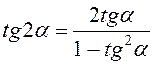4. ;

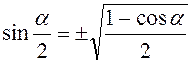5. .

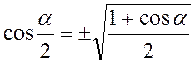Формули перетворення суми та різниці тригонометричних функцій в добуток

1. ;

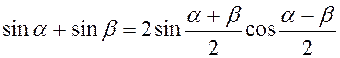2. ;

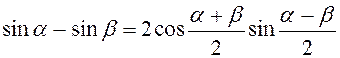3. ;

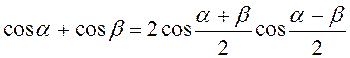4. .

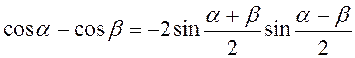Числові функції

Область визначення функції f

X=D(f)

Множина значень функції f

,

E(f)= f(X).

Парна функція

Якщо , то  і .

Непарна функція

Якщо , то  і .

Періодична функція (періоду ω)

Якщо , то ,   і .

Монотонні функції