Збірник завдань для контролю вхідного рівня знань з математики, страница 2

73. Знайти    якщо 

74. Знайти    якщо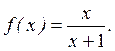 

75. Знайти точку мінімуму функції 

76. Знайти точку максимуму функції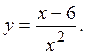 

77٭. До графіка функції 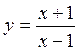     у точці з абсцисою    проведено дотичну. Знайти площу трикутника, утвореного цією дотичною та координатними осями.

78٭. При якому значенні параметра  a  функція     у точці    має мінімум?

79. Через вершину прямого кута  С  трикутника АВС до площини трикутника проведений перпендикуляр  КС, довжина якого дорівнює  4см. Знайти відстань від точки  К до прямої АВ, якщо АС=ВС=8см.

80. Знайти менший з кутів паралелограма, якщо один з його кутів на 20˚ більше другого. Відповідь подати у градусах.

81. Бісектриса гострого кута прямокутного трикутника поділяє катет на відрізки 12 см і 15 см. Знайти суму сторін трикутника.

82. Основа рівнобічного трикутника дорівнює , медіана бічної сторони дорівнює 4. Знайти довжину бічної сторони.

83. З однієї точки кола проведено дві хорди довжиною 10 см та 12 см. Знайти радіус кола, якщо відстань від середини меншої хорди до більшої хорди дорівнює 4 см.

84. Площа рівнобічної трапеції, описаної навколо круга, дорівнює 32 см², гострий кут трапеції дорівнює 30˚. Знайти периметр трапеції.

85٭. В трапеції основи дорівнюють 7 см та 2 см, діагоналі взаємно перпендикулярні, а кут між боковими сторонами дорівнює  45˚. Знайти площу трапеції.

86٭. Вершини прямокутника, вписаного в коло, поділяють його на чотири дуги. Знайти відстані від середини однієї з більших дуг до вершини прямокутника, якщо сторони його дорівнюють 24см і 7см.

87. Сторона основи правильної чотирикутної піраміди дорівнює  см, а її діагональний переріз – прямокутний трикутник. Знайти об’єм піраміди.

88. Ребро правильного тетраедра  DABC дорівнює см. Знайти площу його перерізу, який проходить через ребро  СD  та середину ребра AB.

89٭. Основою паралелепіпеда служить ромб зі стороною а і гострим кутом 30⁰. Діагональ однієї бічної грані перпендикулярна до площі основи, а бічне ребро складає з площиною основи кут 60⁰. Знайти повну поверхню і об¢єм паралелепіпеда.

90٭. В піраміді  SABC  бічні ребра  дорівнюють 2 см,  ÐASB=ÐASC=45˚,  ÐBSC=60˚. Знайти об’єм піраміди.

РОЗВ’ЯЗАННЯ ТИПОВИХ ЗАВДАНЬ

1.Розв¢язати рівняння

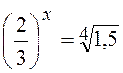
Розв¢язання.

Виконаємо перетворення для приведення до однакової основи:

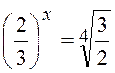
Скористаємося властивостями степеня:

 

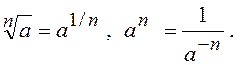
Тоді .

Тоді   .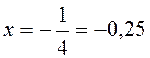 

Відповідь:- 0,25.

2.Розв¢язати рівняння

Розв¢язання.

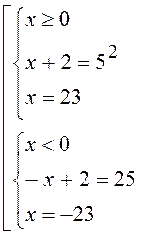
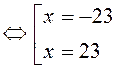
Відповідь:-23,23.

3.Розв¢язати систему рівнянь

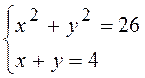
Розв¢язання:

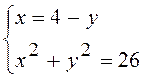
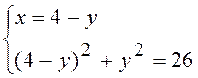
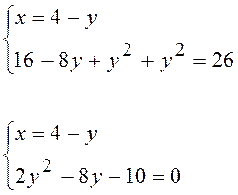
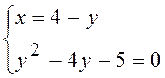
Розв¢яжемо квадратне рівняння:

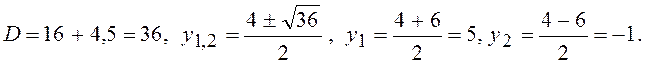
При y = 5 : x = 4 – y = 4 – 5 = -1, при  y =  - 1: x = 4 – y = 4 + 1 = 5 .

Відповідь: ( -1; 5) , (5 , - 1 ).

4. Площа рівнобедреної трапеції, описаної навколо круга, дорівнює  см². Знайти бокову сторону трапеції, якщо відомо, щогострий кут при основі дорівнює .

Розв¢язання.

 

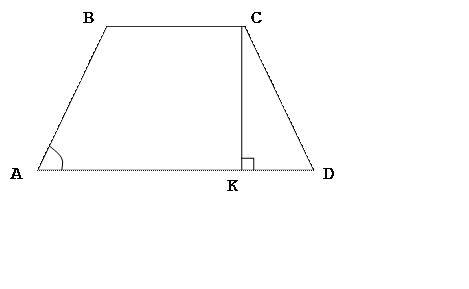За умовою АВ = СD, S_АВСD=32см²

?

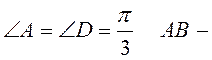Проведемо

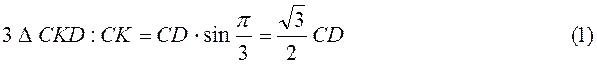
З того, що трапеція описана навколо круга, випливає, що виконується рівність:

АВ + СD =ВC + AD,  а через те, що AB = CD, маємо:  2СD =ВС + AD .

За формулою для знаходження площі трапеції

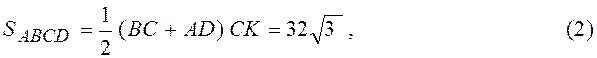
скористаємося (1) та (2):

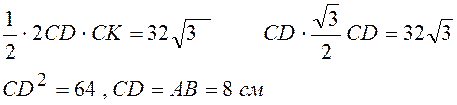
Відповідь: 8 см.

5.Розв¢язати  рівняння

.

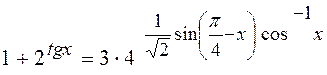Розв¢язання:

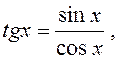звідки OДЗ:cosx ¹ 0 , .

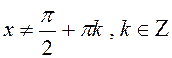Використовуємо формулу

маємо:

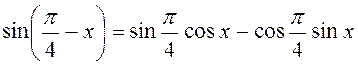
Взявши до уваги, що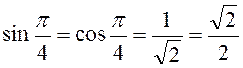

отримаємо:

.

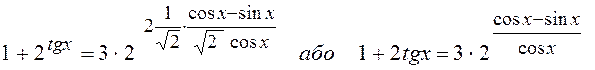Спрощуючи, одержимо:

.

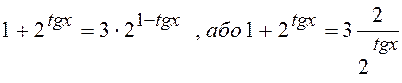Беремо до уваги ОДЗ, позначимо 2^tgx=t.

Тоді .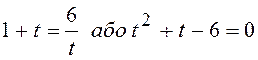

З теореми Вієта маємо:

t₁=2 ; t₂ =-3 .

Так  як  при  будь-яких значеннях функції tgx, то t=-3 не має змісту.

Отже, розглядаємо тільки t=2. Тоді:

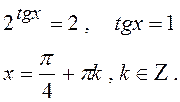
Відповідь: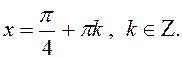

6. Розв¢язати задачу

Кавуни, що привезені на базу, призначені для двох магазинів. Перший магазин одразу приступив до перевезення кавунів і перевозив їх щодня однаковими за масою порціями. Другий магазин приступив до перевезення кавунів на а днів пізніше і також перевозив їх щодня однаковими за масою, але іншими, ніж перший магазин, порціями.

Через b днів, що пройшли від самого початку операцій по перевезенню, на базі залишилася половина первісної кількості кавунів. За скільки днів були вивезені усі кавуни з бази, якщо перевезення закінчилося одночасно і маса кавунів, одержаних першим магазином, дорівнює масі кавунів, отриманим другим магазином.