63. формулы для вычисления свободных членов канонических уравнений;
RiP=(i=1,..,n)
Нахождение свободных членов:
Основа нахождения – грузовое состояние основной системы;
Для образования грузового состояния к основной системе прикладывается заданная внешняя нагрузка.
Способы нахождения:
- перемножение эпюр:
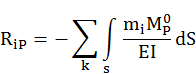
- статический способ:
Основан на рассмотрении равновесия узлов и отдельных частей основной системы грузовой эпюры.
64. формулы для определения окончательных внутренних усилий;
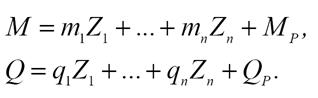
Продольные силы, при известных поперечных силах, определяются из условия равновесия узлов заданной системы.
65. группировка основных неизвестных.
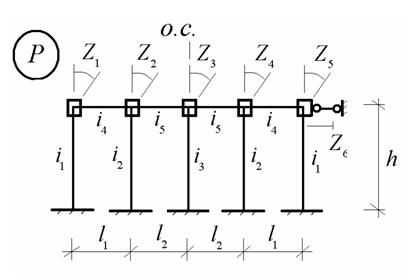
Получение симметричных и антисимметричных основных неизвестных, также как и при расчете методом сил, связано с использованием при- ем группировки однотипных основных неизвестных. Для рассматриваемой рамы выделяются две пары таких величин - углы поворота Z1 , Z 5 и углы поворота Z2 , Z6 , которые искусственно разделяются на симметричные и антисимметричные составляющие. Эти искусственно выделенные две группы величин перемещений и являются новыми основными неизвестными, соответственно, симметричными и антисимметричными. Два оставшихся исходных перемещения Z3 и Z6 , связанных с антисимметричной схемой деформирования рамы, целиком относятся к новым антисимметричным основным неизвестным.
М.12 “Метод конечного элемента”
66. суть метода;
Основная идея метода конечных элементов состоит в том, что рас- считываемая строительная конструкция заменяется совокупностью некоторых элементов, соединенных между собой и с основанием в конечном числе точек. Элементы, на которые разбивается строительная конструкция, называются конечными элементами, а точки их соединения - узлами. При этом внешняя нагрузка заменяется системой эквивалентных узловых сил. Такая дискретизация исходной конструкции и действующей нагрузки позволяет заменить ее расчет расчетом некоторой идеализированной системы с конечным числом степеней свободы. Конечные элементы должны обладать постоянными жесткостными параметрами, а их напряженно-деформированное состояние должно с достаточной точностью описываться некоторыми аналитическими выражениями. Это важно для определения связи между узловыми усилиями и перемещениями.
67. конечный элемент;
Конечные элементы-элементы, на которые разбивается строительная конструкция.
68. узел;
Узлы-точки соединения конечных элементов.
69. типы конечных элементов;
По геометрической форме различают три типа простейших базовых конечных элемента, на которые могут разбиваться различные конструкции: − одномерные; − двухмерные; − трехмерные. Одномерный конечный элемент представляет собой призматический стержень (рис.12.1). Двухмерный конечный элемент может быть двух видов - треугольная пластина (рис.12.2.а) и прямоугольная пластина (рис.12.2.б). Трехмерный конечный элемент представляет собой тетраэдр (рис.12.3)
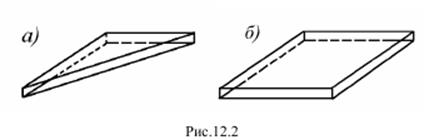
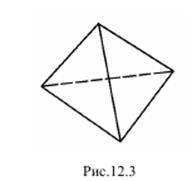
Конечные элементы характеризуются числом узлов и числом узловых реакций. Число узлов конечного элемента зависит от его формы и мерности.
70. вектор перемещений конструкций;
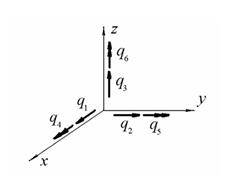

векторы с одинарной стрелкой соответствуют линейным перемещениям, а векторы с двойной стрелкой – угловым перемещениям узлов.
71. вектор нагрузки конструкций;
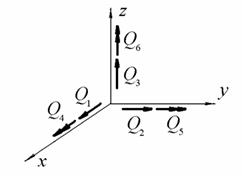
Векторы с одинарной стрелкой соответствуют узловым силам, а векторы с
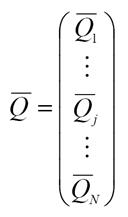
двойной стрелкой – узловым моментам. Вектор нагрузки произвольного j-того узла (j=1,…,N).
72. матрица жёсткости конструкций;
Матрица жесткости конструкции имеет блочную структуру
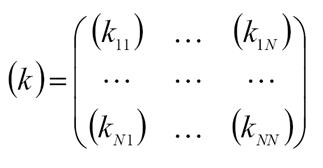
Каждый блок матрицы жесткости конструкции представляет собой под- матрицу единичных реакций, возникающих в произвольном узле, и, в общем случае, имеет размеры 6х6
73. вектор перемещений конечного элемента;
74. матрица жёсткости конечного элемента.
Матрица жесткости отдельного конечного элемента также имеет блочную структуру
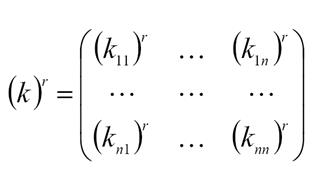
Каждый блок матрицы жесткости отдельного конечного элемента тоже представляет собой подматрицу единичных реакций, возникающих в произвольном узле конечного элемента, и, в общем случае, имеет размеры 6х6.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.