М.8 “ Метод сил”
9. заданная система;
Исходное состояние рамы называется заданной системой.
10. основная система;
Любая статически определимая система, полученная из задданой системы, путём удаления всех лишних связей, для которой соблюдаются требования статической и кинематической эквивалентности.
11. канонические уравнения;
Входящие в это уравнение величины δ11 и Δ1P
являются перемещениями в основной системе по направлению удаленной связи
от действия силы 
1=1
и заданной нагрузки. Для их определения используется формула Максвелла-Мора.
Уравнения имеют кинематическую природу, так как каждое такое уравнение выражает равенство нулю полного перемещения в основной системе по направлению соответствующего основного неизвестного от действия всех основных неизвестных, а также нагрузки, температуры и осадки опор.
δ11 X1 +… + δ1n Xn +Δ1P+Δ1t+Δ1c =0
………………………………………………………………
Δn1 X1 +… + δnn Xn +ΔnP+Δnt+Δnc =0
12. формулы для вычисления коэффициентов канонических уравнений;
В зависимости от соотношений между индексами различают два вида таких коэффициентов. В случае если i = j, то соответствующие коэффициенты называются главными коэффициентами, и они удовлетворяют условию строгой положительности:
δii > 0 (i=1 ,...,n) 
В случае если i ≠ j, то соответствующие коэффициенты называются побочными коэффициентами, и они удовлетворяют условию взаимности:
δij =δji (i, j=1 ,...,n)
13. формулы для вычисления свободных членов канонических уравнений;
Входящие в канонические уравнения частичные перемещения ΔiP, Δit, Δic (i=1 ,...,n) от действия, соответственно, нагрузки, температуры или осадки опор называются свободными членами канонических уравнений.
От действия нагрузки: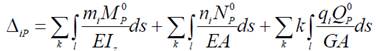 
От действия температуры: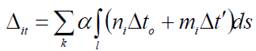 
От осадки опор: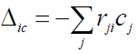 
14. единичные состояния основной системы;
По направлению отброшенных связей, прикладывается единичная нагрузка, от которой строятся эпюры m, q, n.
15. состояния основной системы при приложении внешних воздействий;
Для определения свободных членов канонических уравнений ΔiP
=1(i ,...,n) необходимо рассмотреть основную систему под действием
нагрузки, найти внутренние усилия 
,
,
и
построить их эпюры. Такие внутренние усилия и их эпюры называются грузовыми, а
соответствующая им схема нагружения считается грузовым состоянием основной
системы.
16. методы решения канонических уравнений;
Математической формой канонических уравнений метода сил является система неоднородных линейных алгебраических уравнений:
a11 x1+ a12 x2+ ... +a1n xn = b1
a21 x1+a22 x2+ ...+ a2 nxn=b2 . (8.9)
......................................
an1 x1 + an 2 x2 + ... +ann xn = bn
Связь между величинами, входящими в системы уравнений (8.9) и (8.7), определяется соотношениями:
aij=δij, xj=Xj, bj=-(∆iP+∆it+∆ic)
Поэтому для решения канонических уравнений метода сил применяют численные методы решения систем линейных алгебраических уравнений. При числе основных неизвестных не превышающем 103 обычно применяется метод Гаусса. При большем числе основных неизвестных применяют итерационные методы, например, метод простой итерации.
17. формулы для определения окончательных внутренних усилий;
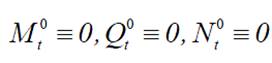
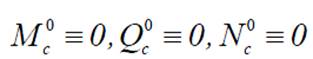
Таким образом, для определения внутренних усилий в заданной системе необходимо, в соответствии с принципом суперпозиции, сложить внутренние усилия, полученные в основной системе от основных неизвестных X1 ,...,X n, заданной нагрузки, температуры и осадки опор. Следовательно, при совместном действии на заданную систему нагрузки, температуры и осадки опор формулы для определения внутренних усилий, с учетом (8.9) и (8.10), имеют вид:
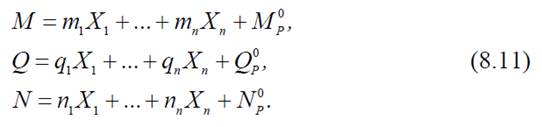
В случае раздельного действия нагрузки, температуры и осадки опор формулы (8.11) принимают вид:
− для нагрузки:
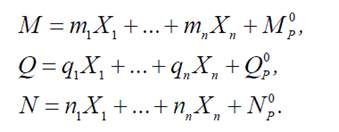
− для температуры или осадки опор:
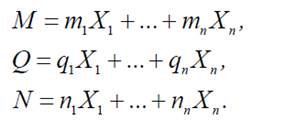
18. проверки метода сил;
Поверки метода сил имеют следующую структуру
Проверки МС
Промежуточные Окончательные
1. Статические 1. Статические
2. Кинематические 2. Кинематические
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.