Введение в теорию расчёта статически неопределимых систем, страница 4

Таким образом, для получения матричной формулы, позволяющей получить вектор основных неизвестных, необходимо сформировать матрицу коэффициентов канонических уравнений и вектор свободных членов от действия нагрузки.

25.  матрица основных неизвестных;

Матрица влияния изгибающих моментов основной системы, связанная с действием нагрузки:

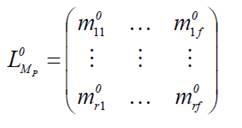
Строим эпюры от единичных нагрузок, приложенных последовательно к сечениям в которых действует дискритизированная внешняя нагрузка. Далее из значений единичных эпюр формируем матрицу основных неизвестных.

26.  матрица податливости основной системы;

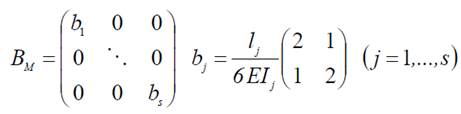
27.  формула для вектора основных неизвестных;

Для определения вектора основных неизвестных с учетом только изгибных деформаций принимает вид:

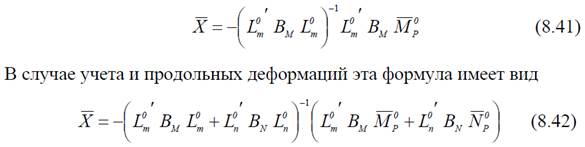
28.  формулы для векторов окончательных внутренних усилий.

L_mp0 - матрица влияния основной системы, связанно            с влиянием действия нагрузки;

L_m⁰, L_m^0/ - матрица влияния изгибающих моментов основной системы, связанной с действием основных неизвестных;

В_m – матрица податливости основной системы.

М.9 “Расчёт двухшарнирной арки”

29.  заданная система;

Заданная система – арка с опорами, имеющая некоторое симметричное очертание согласно заданному закону y=f(x), изменение геометрических характеристик поперечного сечения вдоль оси арки описывается некоторыми заданными функциями A=A(s), Iz=Iz(s), на арку действует нагрузка g(x).

30.  основная система метода сил;

Основная система – получается путём удаления в заданной системе необходимого числа связей для получения статически определимой системы. Трёхшарнирная арка, для которой соблюдается требования её статической и кинематической эквивалентностей с заданной системой и является основной системой метода сил для двухшарнирной арки.

31.  каноническое уравнение метода сил;

δ₁₁  X₁ +Δ_1P =0  ,где     δ_11-   единичный взаимный угол поворот торцов в замковом шарнире  основной системы от действия безразмерного момента X₁=1.

32.  формула для определения коэффициента канонического уравнения метода сил;

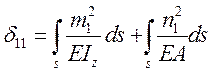
33.  формула для определения свободного члена канонического уравнения;

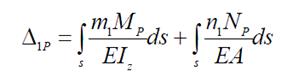
34.  Формулы для определения внутренних усилий в единичном состоянии;

С целью определения единичных внутренних усилий m₁ , n₁ образуем единичное состояние, загружая основную систему безразмерным моментом =1.

 

35.  Формулы для определения окончательных внутренних усилий;

36.  Проверки правильности расчёта двухшарнирной арки.

Для проверки правильности определения опорных реакций и внутренних усилий выполняются 2 проверки – статическую и кинематическую.

Статический метод:

Статическая поверка заключается в проверке равновесия арки в целом при действии на нее заданной нагрузки и опорных реакций. С этой целью составляются три уравнения равновесия:

Кинематическая поверка заключается в проверке соблюдения условия для замкового сечения двухшарнирной арки:

Δ₁ =0

Которое с учетом формулы Максвелла-Мора принимает вид:

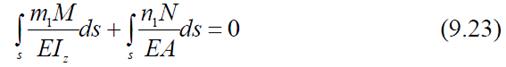
Выполнив с левой частью (9.23) преобразования, аналогичные преобразованиям формул (9.5), (9.6), получим:

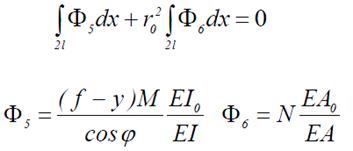
Применяя для вычисления интегралов, входящих в (9.24), формулу метода трапеций, получим окончательное выражение для кинематической поверки:

Входящие в (9.25) 5 Σ и 6 Σ вычисляются по формуле (9.14).

При выполнении условий (9.22) и (9.25) опорные реакции и внутренние усилия считаются найденными правильно.

М-10

37.  неразрезная балка;

Неразрезной балкой называется балка, имеющая не менее 2 пролетов и не прерываемая на всем своем протяжении сквозными разрезами и шарнирами. Пример простейшей балки:

38.  типы неразрезных балок;

·  простые неразрезные балки:

·  неразрезные балки с консолями:

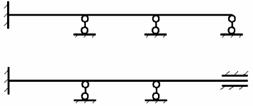·  неразрезные балки с защемляющими опорами:

39.  нумерация опор и пролётов;

Наиболее естественно данная система реализуется при нумерации опор и пролетов простой неразрезной балки. Пример обозначения показан на рис.10.5:

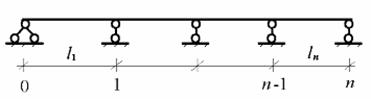
В случае неразрезной балки с консолями последние не включаются в единую систему нумерации пролетов, так как являются статически определимыми участками неразрезной балки. Длины консолей обозначаются независимо, а все остальное обозначается, как и в случае простой неразрезной балки. Пример обозначения показан на рис.10.6: