Введение в теорию расчёта статически неопределимых систем, страница 6

,≤

53.  объемлющая эпюра;

График, описывающие распределение экспериментальных значений  внутреннего усилия от действия временной нагрузки по длине неразрезной балки -  объемлющая эпюра.

54.  способы построения объемлющих эпюр.

Точный способ :построение объемлющих эпюр основано на на использовании линии влияния соответствующего внутреннего усилия. По линиям влияния ,построенным для каждого расчетного сечения, находятся максимальное и минимальное значения внутреннего усилия. Объединение  найденных значений внутренних усилий на одном графике и позволяет получить точное очертание объемлющей эпюры рассматриваемого внутреннего усилия.

Точный способ: построение объемлющих эпюр основан на использовании обычных эпюр внутренних усилий.

Построим объемлющую эпюру изгибающих моментов для трехпролетной  неразрезной балки. Загрузим поочередно каждый пролет временной нагрузкой и, используя моментные фокусные отношения, построим эпюры моментов.

М.11 “Метод перемещений”

55.  кинематическая неопределимость;

Узловые перемещения, подлежащие первоочередному определению, являются основными неизвестными метода перемещений, а их общее число и называется степенью кинематической неопределимости n. Сама же стержневая система считается кинематические неопределимой.

n=n₁+n₂, где  1 n  - число неизвестных угловых перемещений узлов рамы,  2 n - число  неизвестных линейных перемещений узлов рамы, которое характеризует  степень линейной подвижности рамы. 

Число неизвестных угловых перемещений  1 n  равняется числу жестких узлов рамы. Для определения степени линейной подвижности рамы  2 n   во все жесткие узлы  рамы вводятся шарниры. Число степеней свободы,  полученной шарнирно стержневой системы, совпадает со степенью линей- ной подвижности рамы. Следовательно, для рамы, показанной на рис.11.2,  1 2 = n . 

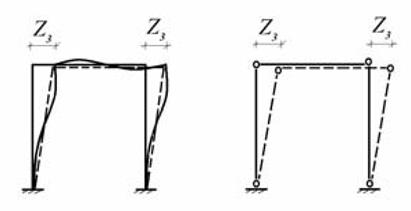
Рамы,  у  которых  могут  возникать  линейные  перемещения  узлов  только за счет изгибных деформаций ее стержней  0 2 ≠ n , принято называть   свободными рамами. Рамы, у которых такие перемещения отсутствуют  0 2 = n , называются несвободными рамами.

56.  основные допущения;

Во-первых, пренебрегают продольными и поперечными деформациями стержней, поскольку при определении перемещений в рамных системах, как правило, учитываются только деформации изгиба. И, во-вторых, ввиду малости перемещений в линейно деформируемых системах, пренебрегают сближением концов изгибаемых стержней.

57.  заданная система;

-исходное состояние системы.

58.  основная система;

Эквивалентность двух систем должна состоять в одинаковости перемещений (кинематическая эквивалентность метода перемещений) и одинаковости внутренних усилий (статическая эквивалентность метода перемещений). Такая эквивалентная система и называется основной системой метода перемещений.

59.  канонические уравнения;

++=0

…………………………

++=0  Полученные уравнения представляют собой систему неоднородных линейных алгебраических уравнений относительно основным неизвестным  ,….

60.  единичные состояния;

Для определения коэффициентов канонических уравнений метода перемещений нужно последовательно загрузить основную систему безразмерными перемещениями       ~

Z=1 ( j=1 ,...,n)

Такие схемы нагружения считаются единичными состояниями основной системы метода перемещения.

61.  формулы для вычисления коэффициентов канонических уравнений;

Свойства: r_ij (i,j=1,..,n) r_ij>0, r_ij= r_ji;

Нахождение коэффициентов:

Для образования единичного состояния последовательно прикладываем перемещение равное единице по направлению основного неизвестного. Результатом является построение единичных эпюр внутренних усилий.

Способы определения:

1)  Перемножение эпюр

Эп. m_i (i=1,..,n)

,

2)  Статический способ

Основан на рассмотрении равновесия узлов и отд-ных частей осн. системы в единичных эпюрах.

62.  грузовое состояние;

Для  определения  свободных  членов  канонических  уравнений R_ip(i=1,…, n) необходимо  рассмотреть основную систему  под  действием  нагрузки и построить эпюры изгибающих моментов  M_р  и поперечных сил  Q_р . Такие эпюры  M_р ,  Q_р  называются грузовыми, а соответствующая им  схема нагружения считается грузовым состоянием основной системы.