Введение в теорию расчёта статически неопределимых систем, страница 5

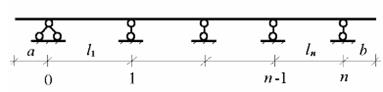
В случае неразрезной балки с защемляющими опорами последние заменяются эквивалентным шарнирно-стержневым изображением. В результате получается простая неразрезная балка с одним или двумя фиктивными пролетами нулевой длины, для которой и производится обозначение опор и пролетов. Пример обозначения показан на рис.10.7:

40.  степень статической неопределимости;

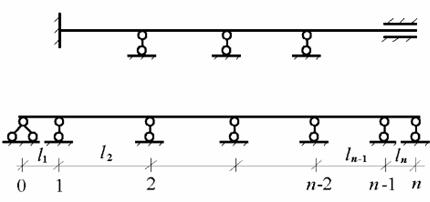
При принятой системе нумерации опор и пролетов степень статической неопределимости неразрезной балки любой разновидности определяется по формуле:

Л=n-1

и совпадает с числом промежуточных опор.

41.  основные системы метода сил для неразрезных балок;

В качестве первого варианта основной системы выберем простую балку, полученную из заданной системы удалением всех промежуточных опор (рис.10.9):

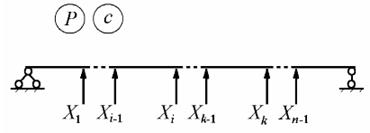
В качестве второго варианта основной системы выберем многопролетную шарнирную балку, полученную из заданной системы введением шарниров во все промежуточные опорные сечения (рис.10.12):

42.  канонические уравнения метода сил;

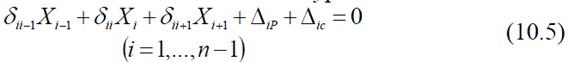
43.  уравнения трёх моментов для нагрузки;

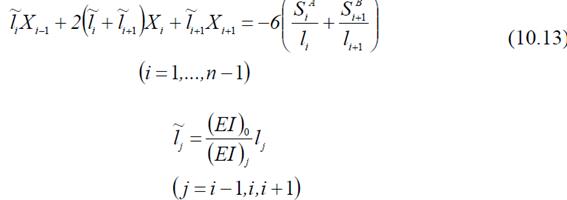
44.  уравнения трёх моментов для осадки опор;

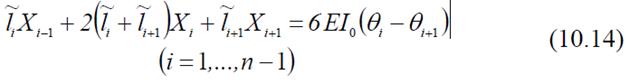
45.  решение системы уравнений трёх моментов;

Система уравнений трех моментов с учетом особенностей структуры первого и последнего уравнений в общем случае имеет вид:

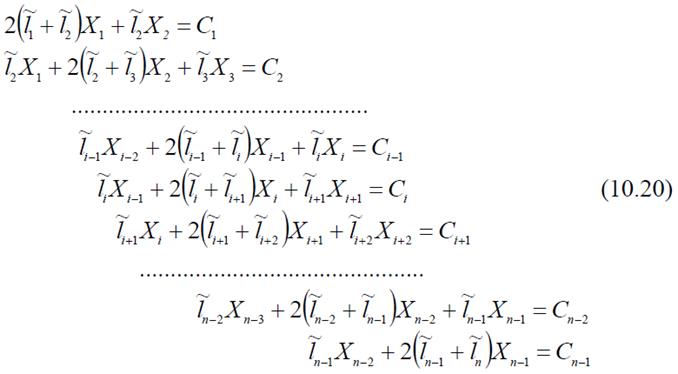
Система уравнений (10.20) является системой линейных алгебраических уравнений с трехдиагональной матрицей коэффициентов, все элементы которой, не лежащие на главной и двух соседних диагоналях, равны нулю.

Решение систем уравнение с трехдиагональной матрицей коэффициентов наиболее просто осуществлять методом прогонки. Алгоритм метода прогонки состоит из прямого и обратного хода.

На первом шаге прямого хода, используя первое уравнение (10.20), неизвестный опорный момент X1 выражается через неизвестный опорный момент X2 и подставляется во второе уравнение. После этого во втором уравнении остаются два неизвестных опорных момента X2 и X3 . Продолжая последовательно процесс выражения неизвестного опорного момента меньшего номера через неизвестный опорный момент большего номера и подстановки его в последующее уравнение, получим последнее уравнение (10.20), содержащим один неизвестный опорный момент Xn-1 .

На первом шаге обратного хода, используя полученное последнее уравнение, находится опорный момент Xn-1 . Затем в обратном порядке находятся все остальные неизвестные опорные моменты.

46.  формулы для определения окончательных M и Q от нагрузки;

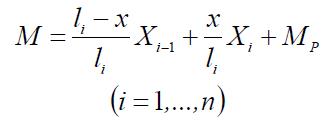
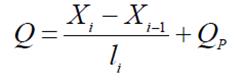
47.  формулы для определения окончательных M и Q от  осадки опор;

M=+  (i=1,…,n);Q=

48.  формула для определения опорной реакции на произвольной опоре неразрезной балки;

+   (i=0,1,…,n);  где -поперечная сила в крайнем левом сечении пролета, примыкающего справа;    - поперечная сила в крайнем правом сечении пролета, примыкающего слева к опоре.

49.  фокальные свойства;

       Первое свойство: Опорные моменты по концам незагруженных пролетов имеют разные знаки.

       Второе  свойство: Отношение опорных моментов по концам незагруженных пролетов не зависит от нагрузки ,а зависит только от жесткостных и геометрических параметров неразрезной балки.

      Третье  свойство: На эпюре моментов в незагруженных пролетах имеется инвариантная нулевая точка ,положение которой не зависит от нагрузки, а полностью зависит только от жесткостных и геометрических параметров неразрезной балки.

   Четвертое  свойство: Опорные моменты в незагруженных пролетах убывают по модулю по мере удаления от загруженного пролета неразрезной балки.

50.  моментные фокусы;

Инвариантная нулевая точка на эпюре моментов незагруженного пролета называется моментным фокусам.

Левым моментным фокусам называется инвариантная нулевая точка на эпюре моментов незагруженного пролета при условии ,что нагрузка располагается справа от этого пролета.

Правым моментным фокусам называется инвариантная нулевая точка на эпюре моментов незагруженном пролете при условии ,что нагрузка располагается слева от этого пролета.

51.  формулы для вычисления моментных фокусных отношений;

          -     - 

=2+/(2-) - левое моментное фокусное отношение

-    =2+/(2-) - правое моментное фокусное отношение

52.  интервал изменения моментных фокусных отношений;