Введение в теорию расчёта статически неопределимых систем, страница 3

3.  Алгебраические и преследуют следующие цели:

- промежуточные  поверки  –  осуществлять  контроль  правильности  выполнения промежуточных этапов расчета;

- окончательные  поверки  –  проверять  правильность  построения  эпюр окончательных внутренних усилий.

19.  упрощения метода сил;

Центральным  моментом  расчета  статически  неопределимых  стержневых конструкций методом сил является составление канонических уравнений  и  их  решение  для  определения  основных  неизвестных.  Поэтому трудоемкость расчета, прежде всего, зависит от числа составляемых канонических  уравнений.  Число  таких  уравнений  равняется  степени  статической  неопределимости  рассчитываемой  стержневой  конструкции  и  для произвольной статически неопределимой стержневой конструкции составляется система n канонических уравнений:

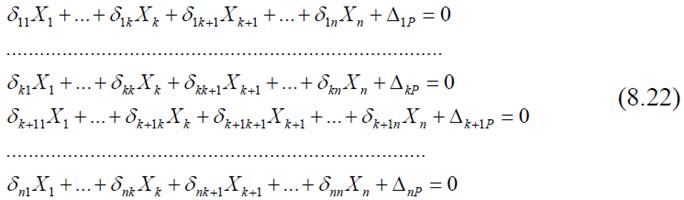
Кроме того, трудоемкость расчета методом сил зависит от числа совместно решаемых уравнений для определения основных неизвестных. Число совместно решаемых канонических уравнений зависит от выбора варианта основной системы метода сил. Следует различать следующие возможные разновидности основных систем метода сил.

Во-первых, обычная основная система, когда для определения основных неизвестных нужно совместно решать все n канонических уравнений системы (8.22). Такой вариант решения канонических уравнений является самым неблагоприятным.

Во-вторых, идеальная основная система.

В-третьих, рациональная основная система.

20.  идеальная основная система;

Идеальная  основная система,  когда система  канонических  уравнений  распадается  на  n  отдельных  уравнений,  содержащих  по одному неизвестному.

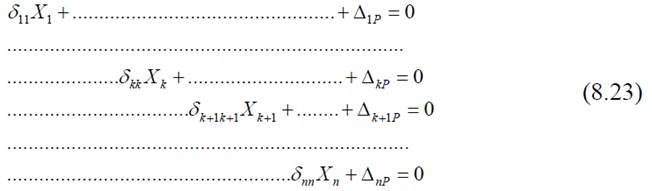
Каждое уравнение (8.23) позволяет независимо найти соответствующее основное неизвестное. Такой вариант решения канонических уравнений является наиболее благоприятным. В принципе, приведение системы канонических уравнений к виду (8.23) возможно для любой статически неопределимой стержневой конструкции. В общем случае трудоемкость процесса приведения канонических уравнений к виду (8.23) достаточна велика.

Однако существуют приемы, позволяющие для статически неопределимых стержневых конструкций частного вида, достаточно просто получать идеальные основные системы метода сил.

21.  рациональная основная система;

В-третьих, рациональная основная система, когда система канонических уравнений распадается на две отельные подсистемы уравнений:

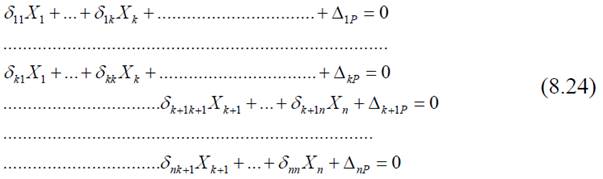
Первая подсистема уравнений содержит основные неизвестные X₁,..., X _k, вторая – X_к+1 ,..., X_n  . Поэтому решение системы канонических уравнений в виде (8.24) позволяет, не сокращая числа неизвестных, найти их независимо по частям.

Одним из приемов получения рациональной основной системы является использование свойств симметрии рассчитываемой статически неопределимой стержневой конструкции. В строительной механике используется понятие геометрической или пространственной симметрии, согласно которому конструкция должна быть инвариантна относительно геометрических преобразований – поворота вокруг оси или отражения в плоскости.

Поэтому признаками симметрии стержневой конструкции относительно некоторой оси являются:

− симметрия общих геометрических размеров;

− симметрия схем узловых соединений и опорных закреплений;

− симметрия жесткостных характеристик конструктивных элементов.

22.  симметричная основная система;

Симметричная стержневая система, в которой для образования рациональной основной системы требуется применять группировку основных неизвестных.

23.  группировка основных неизвестных;

Для симметричных систем общего вида применяют группировку однотипных основных неизвестных и искусственное выделение симметричных и антисимметричных составляющих.В этом случае единичные эпюры изгибающих моментов, m_1, m_2, m₃  связанные с симметричными основными неизвестными, будут иметь симметричные очертания. Единичные эпюры изгибающих моментов m_4, m_5, m₆, связанные с антисимметричными основными неизвесными, будут иметь антисимметричные очертания. Следовательно, все побочные коэффициенты системы канонических уравнений, получаемые при перемножении симметричных единичных эпюр с антисимметричными и наоборот, тождественно равны 0.

24.  Вектор основных неизвестных;