Расчёт переходного процесса в электрической цепи, страница 3

ЗАДАНИЕ  К  КУРСОВОЙ  РАБОТЕ  ПО  ТЕМЕ: расчет переходного процесса в RLC - цепи

1.  Записать, используя Microsoft Excel или Microsoft Word, таблицу исходных данных с примечаниями.

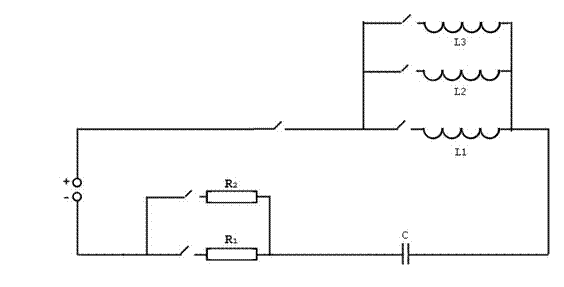
2.  Нарисовать электрическую схему последовательной RLC - цепи, подключаемую ключом к источнику постоянного напряжения с внутренним сопротивлением равным нулю.

3.  Записать все расчетные соотношения, сохраняя обозначения, принятые в математике и электротехнике. Использовать для этой цели встроенный редактор формул, например Microsoft Equation.

4.  Выбрать численный метод решения системы дифференциальных уравнений.

5.  В соответствии с выбранным методом, составить алгоритм решения системы дифференциальных уравнений в виде укрупненной блок-схемы. Выбрать шаг изменения времени .

6.  Провести вычисления в табличном редакторе Excel. Результаты вычислений представить с точностью трех – пяти значащих цифр. Самостоятельно оценить правильность полученных значений, исходя из физики переходного процесса.

7.  По вычисленным  соотношениям  построить  графики  семейств  четырех  функций:  U_C(t, Х),  U_L(t, Х), U_R(t, Х), I(t, Х),  где t - время, Х – изменяющийся исходный параметр, указанный в задании. (Например, емкость С.)

8.  Составить таблицу обозначений используемых величин и их идентификаторов для записи программы на языке программирования (QBASIC). Таблицу набрать в текстовом редакторе Microsoft Word.

9.  Написать программу для решения системы дифференциальных уравнений численным методом, включив в текст программы подробные комментарии. Над текстом программы указать фамилию, шифр группы и номер варианта

10.  Провести вычисления, ответы вывести в виде таблиц, точность представления выбрать аналогичную установленной в Excel. Выведенные результаты должны быть удобны для восприятия, т.е. должны содержать текстовые пояснения.

11.  Сравнить результаты вычислений полученные в Excel, с результатами вычислений по программе на языке QBASIC. Сделать выводы по результатам вычислений, в том числе о характере получившихся зависимостей U_C, U_L, U_R, I от (t,Х).

12.  Оформить пояснительную записку в соответствии со стандартом.

Исходные  данные.

Дана электрическая цепь (рис. 1) состоящая из переменной индуктивности L = 0.8 ё 1.2Гн, емкости C = 1200 мкФ, сопротивления R₁ = 7 Ом и источника питания     e=110 В, как второй вариант рассмотрена схема при условии включения R₂ = 70 Ом, конденсатор полностью разряжается при переключении цепи из одного положения в другое.

Необходимо рассчитать переходный процесс, проходящий в данной электрической цепи.

Дано:

L=0.8ё1.2 Гн с шагом 0,2 Гн

C=1200 мкф

R₁=7 Ом

R₂=70 Ом

e=110 В

Решение дифференциальных уравнений методом Рунге-Кутта.

Общие сведения.

      Обыкновенным дифференциальным уравнением n-го порядка, разрешенным относительно старшей производной, называется выражение вида

                                                                            (1)

 где х - независимая переменная; у – неизвестная функция.

      Известно, что общнн решение (общий интеграл) уравнения (1) записывается в виде

                                                                                                  (2)