Расчёт переходного процесса в электрической цепи, страница 5

Имеется несколько видов формул Рунге-Кутта различного порядка. Формула Рунге-Кутта первого (m=1) порядка совпадает с формулой Эйлера (6), а формула второго (m=2) порядка  - с формулами улучшенного метода Эйлера

                                                                                          (8)

где k₁, k₂ – коэффициенты Рунге-Кутта,  

Погрешность формулы (8) можно записать в виде

                                                     (9)

При каждом m>2 имеется несколько разновидностей формулы Рунге-Кутта. Рассмотрим наиболее распространенные из них. Формулы Рунге-Кутта третьего порядка записываются следующим образом:

                                                       (10)

Формулы Рунге-Кутта четвертого порядка следующие:

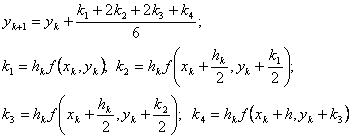                                         (11)

В каждой из приведенных выше групп формул сначала вычисляют значения k₁,k₂,после чего находят y_k+1. Они настолько громоздки, что ими практически не пользуются. Для формул Рунге-Кутта нет точных оценок погрешности при m>2. Известно только, что Формула Рунге-Кутта m-го порядка имеет погрешность порядка h^m+1.

Алгоритм решения системы дифференциальных уравнений RLC-цепи методом Рунге-Кутта четвертого порядка.

Система дифференциальных уравнений RLC-цепи имеет вид:

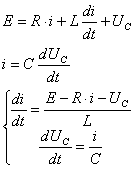
 Схема 1 представляет собой колебательный контур. Период колебаний определяется формулой , которая показывает непосредственную зависимость периода Т от переменной индуктивности L. Выберем наибольший период:

.

Оценим максимальную добротность колебательного контура по формуле: , где - волновое сопротивление. Добротность будет максимальной при максимальном значении индуктивность L. Тогда Расчет  в “EXCEL”

Для случая R=7 Ом

           Таблица 1

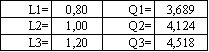Добротность колебательного контура Q>1, значит, колебательный процесс рассматривается на промежутке времени 2T_MAX.

Для случая R=70 Ом

                       Таблица 2

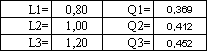Добротность колебательного контура Q<1, значит, колебательный процесс рассматривается на промежутке времени T_MAX.

Исходя из этого, рассмотрим колебательный процесс на промежутке времени. Шаг изменения времени  h возьмем так:. Для более точных расчетов шаг должен быть как можно меньше, то есть период Т должен быть минимальным. Его можно получить при минимальной индуктивности L. Тогда