Сначала была нарисована электрическая цепь с помощью PAINT . Она состоит из двух сопротивлении, переменной индуктивности, емкости и источника питания. После этого с помощью книги “Лабораторные работы по курсу “Вычислительная математика и применение ЭВМ” написал правило решение дифференциальных уравнений методом Рунге-Кутта. Из теории электротехники, был взят, алгоритм решения системы дифференциальных уравнений RLC-цепи методом Рунге-Кутта четвертого порядка. Расчет переходного процесса в RLC - цепи в Excel состоится из определения коэффициенты Рунге Кутта до четвертого порядка.
Коэффициенты Рунге Кутта и их расчетные формулы в Excel.
k1u: C9: =$C$5*L8/$C$2
k1i: D9: = =$C$5*($C$3-$C$4*L8-K8)/$Q$2
k2u: E9: =$C$5*(L8+D9/2)/$C$2
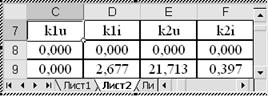 k2i:
F9: =$C$5*($C$3-$C$4*(L8+D9/2)-(K8+C9/2))/$Q$2
k2i:
F9: =$C$5*($C$3-$C$4*(L8+D9/2)-(K8+C9/2))/$Q$2
Напряжение на конденсаторе, Ток в цепи, Напряжение на сопротивлении, Напряжение на индуктивности их расчетные формулы в Excel.
Uc: K9: =K8+(C9+2*E9+2*G9+I9)/6
Ic: L9: =L8+(D9+2*F9+2*H9+J9)/6
Ul: M9: =$C$6*(L9-L8)/$C$5
Ur: N9: =$C$4*L9.
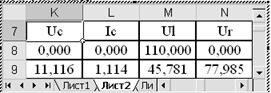
При вычисление в Excel все формулы растягиваются вместе, потому что некоторые вычисление зависит от друг друга. Полностью таблицы результатов расчетов в Excel находятся в приложении ( табл. 1-6 ):
Графики зависимостей были построены по таблице MS Excel при сопротивлении равно R=7 Oм и при сопротивления R= 70 Oм общий вид и характеристики графиков остаются не измененными в обоих случаях. Хотя в случае R1 = 7 Ом на графиках менее заметны резонансные свойства контура в виде синусоидальных колебаний модулирующих основные процессы, происходящие в контуре. Эти процессы более остро выражены в случае R2 = 70 Ом чего и следовало ожидать исходя из законов электротехники, так как во втором случае выше добротность и медленнее происходит затухание паразитных (модулирующих) колебаний. Все полученные результаты стремятся к теоретически возможным процессам электротехники.
Графики зависимостей напряжения на конденсаторе от времени для случая R1=7Ом.
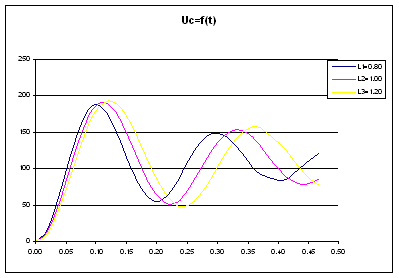
Рис.1 График зависимости напряжения на конденсаторе при различных L.
На графике UC = f(t) видно, что напряжение UС нарастает тем быстрее, чем меньше индуктивность L до значения UC , а далее все происходит наоборот. А так же при различных значениях индуктивности L все графики стремится к данному напряжению, т.е.(110 В.). Все значения напряжения UC достигают значения напряжения E на источнике, то есть UCma x= 110 B.
Графики зависимостей напряжения на индуктивности от времени для случая R1=7Ом.
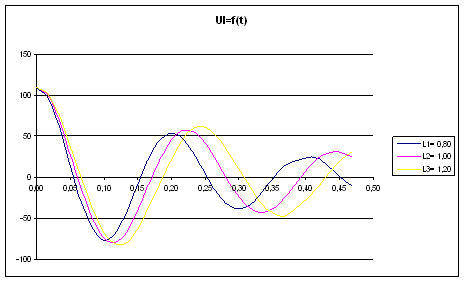
Рис.2 График зависимости напряжения на L.
График UL=f(t) показывает процессы убывания и нарастания напряжения на индуктивности в зависимости от времени. В начальный момент времени напряжение UL на индуктивности имеет максимальное значение. С течением времени напряжение UL на индуктивности стремится к нулю. Из рис. 2 видно, что чем меньше значение индуктивности тем быстрее напряжение на ней достигает установившегося значения.
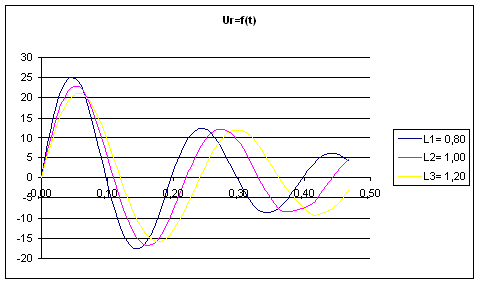
График зависимостей напряжения на сопротивление от времени для случая R1=7Ом.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.