Электромагнитно связанные линии передачи и их применение в антенных системах, страница 7

К настоящему времени изданы справочники, учебники, учебные пособия и выпущены компакт-диски, где подытожены основные результаты проведенных ранее исследований. Поэтому, если в качестве элементов и узлов проектируемых антенных систем будет решено по тем или иным соображениям использовать классические решения, то рекомендуется обратиться к материалам работ [11–26].

Устройства на связанных линиях с экранированными фрагментами были предложены в первой половине 60-х годов [27], затем совершенствовались [28, 29], хотя широкого применения так и не получили. Интерес к ним существенно возрос в последнее десятилетие в связи с прогрессом в микроэлектронных технологиях и активным освоением многослойных (multi-layer, multilevel – многоуровневых) металло-диэлектрических структур [30, 31]. Результаты этих работ получены как квазистатическими методами, так и в строгой электродинамической постановке задач.

Свое место в этих исследованиях занял подход, основанный на представлении многослойных структур с полностью экранированными фрагментами в виде редко используемого в диапазоне СВЧ последовательного соединения многополюсников. При этом используется «вертикальная» декомпозиция (разделение) проектируемого устройства, а его анализ и синтез ведутся с применением классических матриц сопротивлений. Этот подход, постепенно формирующийся с середины 90-х годов [32–36], представляется весьма эффективным и не менее перспективным, чем многомодовый подход, описанный в работах [37, 38]. Ниже излагаются основы этого подхода и результаты его использования при проектировании ранее не описанных в литературе микроволновых узлов новой структуры. В изложении широко используется матрица сопротивлений [z] отрезка связанных линий, впервые сформированная в работе [39] (русский перевод – работа [40]). В принципе эту матрицу можно получить в результате пересчета матрицы  передачи (выражение (1.39)). Однако простота и ясность работы [39], ставшей уже классической, достойны того, чтобы вновь продемонстрировать изящность этого метода формирования матрицы сопротивлений и в наше время.

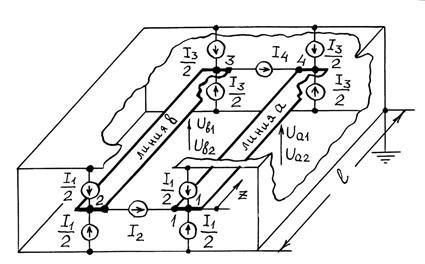
Итак, согласно [39] анализируется структура из двух одинаковых связанных линий, изображенная на рис. 2.1. Обе линии возбуждаются на каждом конце одновременно пятью синхронизированными генераторами тока с соответствующими комплексными амплитудами (напоминание: символ «m» и «точка» в обозначениях комплексных амплитуд токов и напряжений здесь и далее опущены). Четыре генератора тока   возбуждают в линиях синфазные (четные) волны тока, в результате чего на обеих линиях создаются напряжения с комплексными амплитудами:

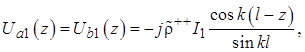
               (2.1)

где  – волновое (характеристическое) сопротивление любой из линий при синфазном возбуждении (равных токах в положительном направлении оси z);  – длина отрезка. Аналогично генераторы тока  создают на обеих линиях напряжения с комплексными амплитудами

                        (2.2)

Рис. 2.1

Генераторы тока  создают в линиях противофазные (нечетные) волны тока с комплексными амплитудами напряжений вдоль линий:

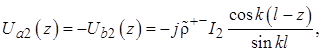            (2.3)

                   (2.4)

где  – волновое сопротивление любой из линий при противофазном возбуждении (равных токах в противоположных направлениях).

Берем за положительное направление суммарных токов   в плечах 1–4 направление внутрь восьмиполюсника (рис. 2.2):

Решив эту систему уравнений относительно токов   можно найти, что

                                         (2.5)

Так как генераторы тока имеют бесконечное внутреннее сопротивление, то каждое из напряжений плеч  , положительные направления и обозначения которых на рис. 2.2 соот

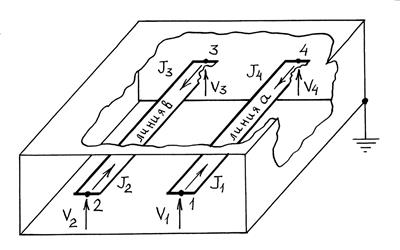
Рис. 2.2

ветствуют англоязычной литературе, есть сумма всех составляющих   (i = 1…4) соответствующего плеча:

 при

     при

    при                       (2.6)

  при  

Если (2.1) – (2.5) подставить в (2.6), то коэффициенты при  будут являться элементами матрицы сопротивлений [z] итоговой системы:   где Т – знак транспонирования. В результате получаем

           (2.7)