Электромагнитно связанные линии передачи и их применение в антенных системах, страница 3

Пусть продольная координата  вдоль пары неодинаковых линий передачи направлена навстречу потоку электромагнитной энергии (рис. 1.2). Такое направление упрощает процедуру формирования уравнений, так как гораздо реже используется знак «–», который не может быть опущен по умолчанию. Термин «регулярные линии передачи» означает, что как поперечные геометрические размеры линий, так и параметры диэлектрика и проводников не зависят от продольной координаты [7]. Термин «регулярные» (а в дальнейшем и «нерегулярные») представляется оправданным и более удачным (адекватным) по сравнению с менее удачным (но часто используемым) термином «однородные» («неоднородные»), поскольку регулярные линии могут иметь как многослойное (неоднородное) диэлектрическое заполнение, так и однородное (как бы «однослойное»).

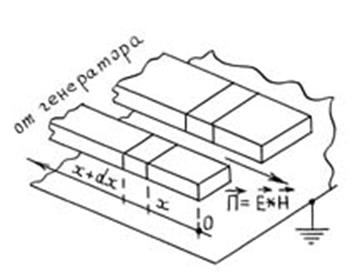
Рис. 1.2

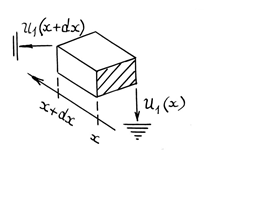
При формировании дифференциальных уравнений используются понятия погонных (на единицу длины) емкостных   и соответствующих по смыслу погонных индуктивных   коэффициентов, обозначенных прописными буквами. Тогда на участке  линии будут иметь параметры   . Применим к фрагменту линий на участке от    до    (рис. 1.3) закон Кирхгофа [1], согласно которому напряжение    равно

                 (1.9)

где  – ЭДС самоиндукции первой линии;   – ЭДС взаимоиндукции. После переноса  влево можно записать

      (1.10)

Наличие в последнем уравнении частных производных означает, что напряжение и токи в линиях являются функциями двух переменных: продольной координаты и времени. При этом изменением величины тока на входе и выходе элемента  линий можно пренебречь как величиной второго порядка малости [8].

Рис. 1.3

Поскольку сигнал любой формы представим суперпозицией отдельных гармонических составляющих, то далее целесообразно использовать аппарат комплексных представлений соответствующих гармонических функций напряжения и тока. Переходя к комплексному представлению  гармонической величины , определяемому как произведение комплексной амплитуды  и «множителя вращения»  (), уравнение (1.10) можно записать как

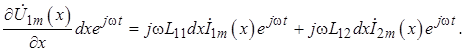
После упрощения оно примет вид (от символа частной производной целесообразно вернуться к обычному символу первой производной):

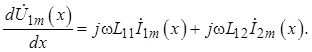                (1.11)

Аналогично составляется уравнение для второй линии:

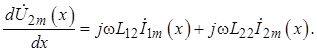              (1.12)

Рассмотрим теперь рис. 1.4, где поступающий ток    растекается по двум направлениям: вдоль линии течет ток   ; в поперечной плоскости, перпендикулярной линиям, растекаются токи смещения в диэлектрике, суммарная величина которых обозначена  :

                       (1.13)

Величина    определяется из базовой системы уравнений (1.1), записанной для участка линий :

Рис. 1.3

 

           (1.14)

Из первого уравнения последней системы находится ток смещения:

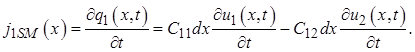
Далее, переходя к комплексным представлениям, получаем

 (1.15)

Из уравнения (1.13) следует, что

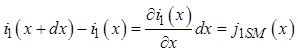
или в комплексных представлениях

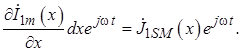                (1.16)

Сопоставляя (1.15) и (1.16), можно записать уравнение не только для приращений, но и для производных (вновь возвращаясь к символу первой производной):

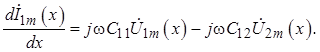         (1.17)

Аналогично формируется дифференциальное уравнение для второй линии:

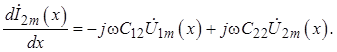          (1.18)

Полученные дифференциальные уравнения (1.11), (1.12), (1.17) и (1.18) называются телеграфными уравнениями для пары связанных регулярных линий передачи. Это объясняется исторически первым применением линий для передачи телеграфных сигналов. Пределом применимости телеграфных уравнений является условие, при котором длина волны в окружающем диэлектрике становится соизмеримой с поперечными размерами (ширина, зазор) линий.

1.3.  Решение телеграфных уравнений. Матрица передачи отрезка связанных линий

В результате решения телеграфных уравнений определяются законы изменения амплитуд и начальных фаз колебаний напряжения и тока (т. е. изменения их комплексных амплитуд) в зависимости от продольной координаты. Разделяя в уравнениях (1.11), (1.12), (1.17) и (1.18) переменные и преобразуя коэффициенты, получим обобщенное дифференциальное уравнение четвертого порядка: