Электромагнитно связанные линии передачи и их применение в антенных системах, страница 11

где      – электрическая длина отрезка кабеля;   – опорная частота отрезка, при которой  .

Воспользовавшись формулами пересчета элементов матриц восьмиполюсников [9], можно сформировать необходимую для дальнейшего анализа матрицу рассеяния  отрезка кабеля «над землей»:

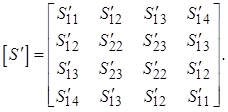                     (2.15)

Далее к матрице  применяется процедура понижения ее размера до величины 2 ´ 2 элементов за счет подключения к плечам 2′ и 3′ отрезка кабеля нагрузок с коэффициентами отражения    или  . Эта процедура подробно описана в работе [9], и ее применение позволяет записать соотношения для элементов  , связанных с оставшимися плечами  1′ и 4′ отрезка:

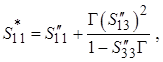
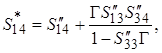                   (2.16)

где

           

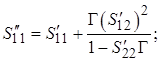
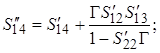
(2.17)

           

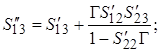
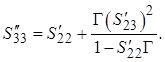
В результате после подстановки в последние соотношения вместо    значений   или   (формулы (2.12)) находятся элементы матриц рассеяния

    

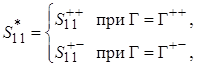
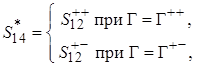
которые с учетом (2.8) определяют итоговые значения элементов матрицы рассеяния  в целом НФ. Эти элементы представляют собой комплексные передаточные функции напряжения соответствующих трактов и входные коэффициенты отражения плеч при подключении к НФ источника сигнала и нагрузок, сопротивления которых равны волновому сопротивлению  подводящих линий.

Программирование описанного алгоритма анализа не встречает затруднений, что позволяет визуально на экране монитора одновременно наблюдать и оценивать частотные характеристики всех модулей элементов матрицы рассеяния (2.8) НФ. В результате проведенного анализа для различных значений  при одинаковых опорных частотах    было установлено, что все они симметричны относительно вертикали в точке    и отличны от нуля в интервале  . Однако уровни отраженного сигнала в плечах   и проходящего сигнала в диагональных трактах 1  4 и 2  3   существенно меньше уровней сигналов в трактах 1  2 (3  4,  и 1 3 (2  4, . Это позволило надеяться на возможность уменьшения    и    до пренебрежимо малой величины за счет привлечения стандартных процедур параметрической оптимизации (поиска экстремума функции многих переменных). В случае успешного результата параметрического синтеза предлагаемое на рис. 2.10 четырехплечее устройство может быть отнесено по общепринятой классификации [9] к восьмиполюсникам с направленностью 2-го типа.

Задача параметрического синтеза формулируется аналогично предыдущему фильтру в стандартной постановке и сводится к отысканию оптимальных значений компонент вектора  варьируемых параметров, образованного волновыми сопротивлениями устройства, приведенного на рис. 2.10: . 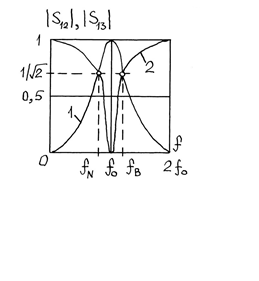Оказалось, что значения    и    пренебрежимо малы не только в полосе оптимизации  , но и во всей полосе частот существования Т-волны, а частотные характеристики    и   имеют период  и удовлетворяют всем критериям фильтрового типа, в том числе соотношению  . В качестве примера на рис. 2.13 (поз. 1 – , поз. 2 – ) представлены эти характеристики для значений  Ом,  Ом,   Ом. Поэтому предложенное на рис. 2.10 устройство может быть отнесено к классу направленных фильтров с одним кольцевым резонатором.

Рис. 2.13

Результаты решения задачи параметрической оптимизации представлены на рис. 2.14 в виде зависимостей электрических параметров – волновых сопротивлений (кривая 1 – ; кривая 2 – ; кривая 3 – ) – фильтров от относительной полосы пропускания   тракта 1 2 по уровню половинной мощности (3 дБ), рассчитываемой с учетом обозначений рис. 2.13 как . Эти результаты используются для расчета геометрических размеров многослойных полосковых линий. В общем, синтез однопетлевого НФ может быть выполнен по любой из двух амплитудно-частотных характеристик –  или  (соответствующие затухания определяются согласно [9] как:  или , дБ). Однако чаще всего его проводят по затуханию полосно-пропускающего тракта  12; этим объясняется выбор переменной по оси абсцисс на рис. 2.14.