Электромагнитно связанные линии передачи и их применение в антенных системах, страница 5

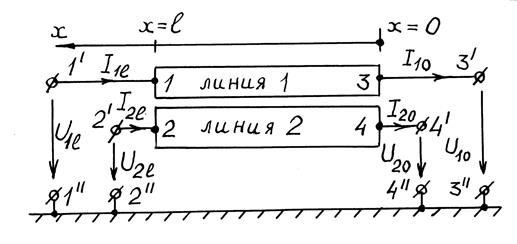
Рис. 1.5

Проиллюстрируем процедуру нахождения постоянных  в (1.29). Из (1.29), (1.11) и (1.32)  при  получаем

Отсюда

  (1.34)

Далее подставляем найденные значения  в (1.30), приводим подобные члены и переходим от показательных функций к тригонометрическим. в результате получаем

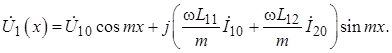          (1.35)

Аналогично составляются и решаются пары уравнений для остальных констант (), Прежде чем записать итоговые результаты этого решения, целесообразно отметить, что в соотношении (1.35) величины  имеют размерность сопротивления:

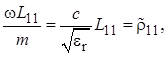
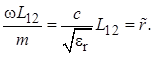               (1.36)

При этом в выражениях для остальных постоянных будут фигурировать:

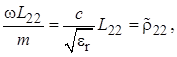
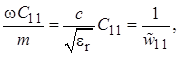
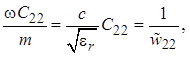
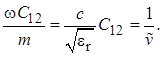              (1.37)

Знак «тильда» («волна» над символом) в последних выражениях обозначает ненормированный параметр, имеющий размерность сопротивления. Теперь с целью еще большего сокращения записи опустим здесь и далее «точку» в обозначениях комплексных амплитуд. Таким образом, несмотря на отсутствие в дальнейших выражениях «точек» и символов «m», они все-таки обозначают комплексные амплитуды.

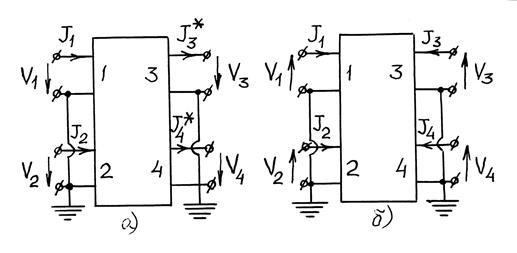
Учитывая принятую на рис. 1.5 нумерацию плеч и полюсов, переходим к более привычным для теории цепей обозначениям токов и напряжений:

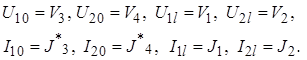         (1.38)

Положительные направления этих величин указаны стрелками на рис. 1.6а, причем токи правой стороны восьмиполюсника направлены от его границы к нагрузкам, подключаемым к соответствующим полюсам (клеммам). В этих обозначениях с учетом (1.36) и (1.37) связь напряжений и токов в плечах отрезка связанных линий геометрической длины  (т. е. при ), номера 1 – 4 которых указаны на рис. 1.6а внутри восьмиполюсника, приобретает вид

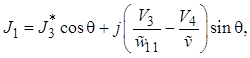
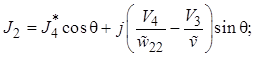
Коэффициенты этих уравнений формируют классическую (цепную) матрицу передачи [a] восьмиполюсника, широко используемую во многих приложениях:

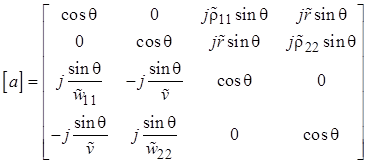 .         (1.39)

Эта матрица связывает комплексные амплитуды напряжений и токов левой (генераторной) стороны восьмиполюсника с комплексными амплитудами тех же гармонических величин правой его стороны. Полезно отметить, что в англоязычной литературе всюду принято считать положительным для токов правой стороны направление от полюсов (клемм) внутрь восьмиполюсника (рис. 1.6б):  Кроме того, принято начало стрелок, обозначающих напряжение, совмещать с полюсом низкого (в частности, нулевого) потенциала. Именно эти обозначения применены на рис. 1.6б. В русскоязычной литературе такого единообразия обозначений нет, по-видимому это объясняется традициями разных научно-технических школ. Эти особенности выбора обозначений положительных направлений, а также возможную смену нумерации плеч (полюсов) и направления отсчета продольной координаты  следует в обязательном порядке учитывать при работе с первоисточниками (статьями, патентами, книгами) во избежание недоразумений. Так, например, матричная форма записи уравнений в [a]-параметрах для ряда русскоязычных работ [3, 9] и всех англоязычных работ соответственно имеет вид

      Рис. 1.6

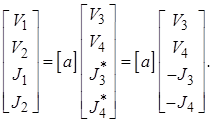
Сформированная матрица передачи (1.39) может быть использована для нахождения всех других матриц восьмиполюсника, включая волновые матрицы передачи и рассеяния. При этом необходимо воспользоваться соответствующими формулами пересчета, приведенными в литературе по теории электрических и радиотехнических цепей, например в работах [3, 5, 6, 9, 10].

1.4.  Расчет геометрических размеров

связанных линий

При практической реализации устройств на связанных линиях используются следующие основные конфигурации, классифицируемые по их поперечным сечениям:

– круглые стержни в прямоугольном (а) или цилиндрическом (б) корпусах (рис. 1.7);

– прямоугольные стержни в прямоугольном корпусе (рис. 1.7в);