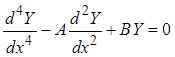Электромагнитно связанные линии передачи и их применение в антенных системах, страница 4

,                         (1.19)

где величина Y имеет смысл одной из четырех функций   переменной  . Коэффициенты А и В связаны с погонными параметрами соотношениями

  (1.20)

                (1.21)

Решение уравнения (1.19) ищется в форме , где  – пока еще не определенные коэффициенты. Для их определения подставляем искомую форму  в (1.19) и получаем характеристическое уравнение , решение которого дает постоянную распространения:

                           (1.22)

Таким образом, постоянная распространения формально может иметь четыре значения:  Общее решение равно сумме всех частных решений:

 (1.23)

Следует учесть, что в линиях не могут распространяться волны с разными скоростями, так как существовать может лишь волна Т-типа, что в математической формулировке означает . Последнее соотношение приводит к частным решениям дифференциального уравнения четвертого порядка  вида  . Однако в курсе лекций доказывается, что такое решение не удовлетворяет соответствующим уравнениям второго порядка. По этой причине решения вида  из рассмотрения исключаются и в дальнейшем используются лишь решения    без линейных множителей . В результате требование   приводит, как следует из (1.23), к уравнениям  Подставив в них значения А и В из (1.20), получаем

                (1.24)

где  Решая уравнение (1.24) относительно  , находим

                    (1.25)

Величина  может быть только вещественной, так как вещественны  С другой стороны, коэффициент  всегда меньше единицы, так как погонные емкости линий  при синфазном возбуждении только положительны. Поэтому   и величина  будет вещественна лишь в двух случаях: либо  либо  Но вариант  невозможен согласно (1.24). Остается принять  и, следовательно,   Тогда из (1.21), (1.24) получаем:

      ;       (1.26)

т. е.: 

Таким образом, анализ решения телеграфных уравнений свидетельствует о том, что погонные параметры линий с волной Т-типа между собой жестко связаны и нельзя говорить об их произвольном выборе. Произвольно могут выбираться поперечные геометрические размеры связанных линий, однако при любых размерах соотношение (1.26) будет иметь место.

Продолжая анализ связанных линий, в выражении для А (1.20) положим   и  . Тогда   и из (1.24) получаем

                            (1.27)

С другой стороны, постоянная распространения Т-волн в диэлектрике:  где  – скорость света в пустоте;  – текущая частота;  – относительная диэлектрическая проницаемость среды (диэлектрика), окружающей связанные линии. Таким образом,

               (1.28)

Из соотношений (1.26) и (1.28) следует связь погонных параметров между собой:

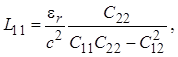
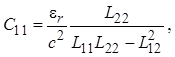
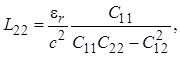
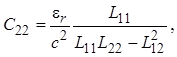
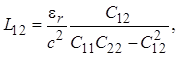
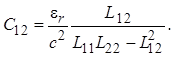
Перейдем к определению классической матрицы передачи [a] отрезка связанных линий. Эта матрица широко применяется при анализе частотных и временных характеристик проектируемых микроволновых устройств на отрезках связанных линий произвольной длины. Прежде всего отметим, что отрезок линий передачи с электромагнитной связью принято рассматривать как восьмиполюсник (четырехплечее устройство). На рис. 1.5 полюса обозначены цифрами со штрихами, при этом цифры с двумя штрихами относятся к полюсам, лежащим на заземленной поверхности и являющимся эквипотенциальными. Пары полюсов с одним и двумя штрихами образуют соответственно плечи 1, 3 для первой линии и плечи 2, 4 для второй. Выше было показано, что напряжения и токи в каждой линии определяются выражениями (см. (1.23) и (1.27))

        (1.29)

        (1.30)

где – волновое число;  (с соответствующими индексами) – постоянные, которые должны быть определены исходя из конкретных граничных условий задачи; для сокращения записи индекс «m» в обозначениях комплексных амплитуд здесь и далее опускается:

При определении матрицы передачи в качестве граничных условий используются токи и напряжения на концах отрезка связанных линий длиной

при              (1.32)

при               (1.33)