Электромагнитно связанные линии передачи и их применение в антенных системах, страница 2

При анализе электромагнитно связанных линий (составлении и решении дифференциальных уравнений) на определенном этапе используются соотношения из электростатики. Поэтому рассмотрим два произвольных проводящих заряженных тела 1 и 2 над «землей» (рис. 1.1), имеющих заряды  и потенциалы  соответственно. Из курса радиофизики известна следующая система уравнений:

                               (1.1)

где  – собственные,  – взаимные емкостные коэффициенты. Знак «–» в уравнениях отражает тот факт, что индуцированный (наведенный) заряд противоположен по знаку наводящему заряду. В обратимых системах   Собственные емкостные коэффициенты могут быть рассчитаны по какой-либо методике и/или измерены стандартными методами, если учесть, что из (1.1)

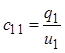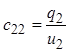    при           при          (1.2)

Иными словами, при отыскании  тело 2 соединяется с «землей» (корпусом прибора) и имеет нулевой потенциал, а при расчете  с корпусом соединяется тело 1. Однако такой подход нерационален при расчетах или измерениях взаимных коэффициентов, так как из условий

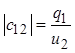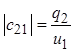   при         при         (1.3)

следует, что необходимо измерять заряд того проводника (тела), который соединяется с корпусом. Поэтому, несмотря на то, что система (1.1)  часто используется в последующих этапах анализа, ее коэффициенты  рассчитываются другим, более практичным путем, исходя из следующих соображений.

Дополним уравнения (1.1) слагаемыми противоположного знака, дающими в сумме нуль и не меняющими суть исходных уравнений:

                   (1.4)

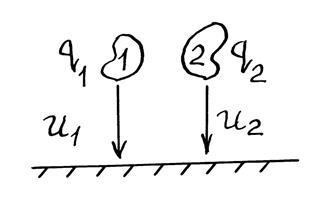
Рис. 1.1

Если сгруппировать в (1.4) слагаемые, помеченные одной линией, то имеем

    (1.5)

а если сгруппировать слагаемые, подчеркнутые одной линией сверху и двумя линиями снизу, то получим

  (1.6)

Из систем (1.5) и (1.6) следует

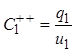    при               при  

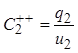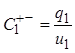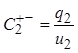  при         при       (1.7)

Таким образом, при расчетах и измерениях емкостных коэффициентов  (i = 1, 2) соединять проводники 1 и 2 с «землей» не требуется. Наоборот, оба проводника должны быть изолированы от корпуса и иметь равные по величине потенциалы  с одинаковыми (для ) или противоположными (для ) знаками.

При анализе высокочастотных режимов работы связанных линий при гармонически изменяющихся во времени процессах (зарядах, токах, потенциалах и т. п.) рассматриваться будут так называемые «синфазное» (++) и «противофазное» (+ – ) возбуждения связанных проводников (отрезков линий передачи). При этом каждая точка сечения обеих линий передачи плоскостями, перпендикулярными к направлению распространения энергии (так называемые «референсные» или «отсчетные» плоскости [5, 6]), будет иметь гармонически изменяющийся во времени одинаковый по модулю потенциал равного (++) или противоположного (+ – ) знака. В принципе одинаковые потенциалы могут быть и отрицательными (– –); однако в литературе принято только одно обозначение, а именно (++). В заключение приводится связь емкостных коэффициентов базовой системы (1.1) с коэффициентами   синфазного и противофазного возбуждений, следующих из (1.5), (1.6):

           (1.8)

Как будет ясно из дальнейшего изложения, расчет геометрических размеров связанных линий (т. е. фактически всех ключевых размеров проектируемого устройства) проводится в настоящее время, как правило, исходя из погонных емкостей (волновых сопротивлений) линий при синфазном и/или противофазном возбуждениях. Полезно также отметить, что синфазный и противофазный режимы часто называются соответственно «четный» (even) и «нечетный» (odd).

1.2. Формирование дифференциальных уравнений

связанных регулярных линий передачи