3 Силовой анализ
3.1 Построение расчетной модели.
Определим массы всех звеньев механизма.
Масса кривошипа 1:
![]()
Масса шатуна 2:
![]()
Масса шатуна 3:
![]()
Масса ползуна 4:
![]()
Масса ползуна 5:
![]()
Модуль силы тяжести:
![]() (3.1.1)
(3.1.1)
где ![]() – масса
i-того звена, кг;
– масса
i-того звена, кг; ![]() –
ускорение свободного падения центра масс звена равное
–
ускорение свободного падения центра масс звена равное ![]() .
.
Силы тяжести кривошипа 1, шатуна 2, 4 и ползуна 3, 5:
![]()
![]() ;
;
![]() ;
;
![]()
![]()
Модуль силы инерции:
![]() (3.1.2)
(3.1.2)
где ![]() – масса i-тогозвена, кг;
– масса i-тогозвена, кг; ![]() – ускорение центра масс i-того звена, м/с2;
– ускорение центра масс i-того звена, м/с2;
Ускорения центра масс найдем по выражению:
![]() (3.1.3)
(3.1.3)
где ![]() – отрезок изображающий на плане
ускорений вектор ускорения центра масс, мм;
– отрезок изображающий на плане
ускорений вектор ускорения центра масс, мм; ![]() –
масштабный коэффициент плана ускорений, м/(
–
масштабный коэффициент плана ускорений, м/(![]() ).
).
Длину отрезка ![]() найдем, замерив соответствующий отрезок на
плане ускорений (лист 1).
найдем, замерив соответствующий отрезок на
плане ускорений (лист 1).
Ускорения центра масс шатуна 2 найдем по выражению (3.1.3):
![]() .
.
Ускорения центра масс шатуна 4:
![]() , где
, где ![]() – отрезок, соединяющий точки
– отрезок, соединяющий точки ![]() и
и ![]() на плане
ускорений и изображающий вектор ускорения центра масс
на плане
ускорений и изображающий вектор ускорения центра масс ![]() .
.
Ускорения центра масс ползуна шатуна 3:
![]() , где
, где ![]() – отрезок, соединяющий точки
– отрезок, соединяющий точки ![]() и
и ![]() на плане
ускорений и изображающий вектор ускорения центра масс
на плане
ускорений и изображающий вектор ускорения центра масс ![]() .
.
Ускорения центра масс ползуна шатуна 5:
![]() , где
, где ![]() – отрезок, соединяющий точки
– отрезок, соединяющий точки ![]() и
и ![]() на плане
ускорений и изображающий вектор ускорения центра масс
на плане
ускорений и изображающий вектор ускорения центра масс ![]() .
.
Силы инерции центра масс шатуна 2, 4 и ползуна 3, 5:
![]() ;
;
![]() ;
;
![]()
![]()
Линия действия векторов сил
инерции ![]() ,
, ![]() ,
, ![]() ,
, ![]() лежат
на прямых, являющихся параллельными линиям действия векторов ускорений центров
масс
лежат
на прямых, являющихся параллельными линиям действия векторов ускорений центров
масс ![]() ,
, ![]() ,
, ![]() ,
, ![]() соответственно.
Направление вектора сил инерции противоположно направлению вектора ускорения центра
масс.
соответственно.
Направление вектора сил инерции противоположно направлению вектора ускорения центра
масс.
Момент от сил инерции:
![]() (3.1.5)
(3.1.5)
где ![]() момент инерции центра масс
момент инерции центра масс ![]() -го звена,
-го звена, ![]() ;
; ![]() угловое ускорение
угловое ускорение ![]() -го
звена,
-го
звена, ![]() .
.
Так как угловое ускорение
кривошипа 1, ползуна 4 и 5 равно нулю ![]() , то
момент инерции соответствующих звеньев тоже равен нулю
, то
момент инерции соответствующих звеньев тоже равен нулю ![]()
Момент инерции центра масс ![]() -го звена:
-го звена:
![]() (3.1.6)
(3.1.6)
где ![]() масса
масса ![]() -го
звена, кг;
-го
звена, кг; ![]() длинна
длинна ![]() -го
звена, м.
-го
звена, м.
Момент инерции центра масс шатуна 2 и 3:
![]()
![]()
Момент от сил инерции шатуна 2 и 3:
![]()
![]()
Момент от сил инерции ![]() и
и ![]() направлен
противоположно направлению действию углового ускорения
направлен
противоположно направлению действию углового ускорения ![]() и
и
![]() соответственно. Для определения действия
углового ускорения
соответственно. Для определения действия
углового ускорения ![]() и
и ![]() перенесем
вектор тангенциального ускорения
перенесем
вектор тангенциального ускорения ![]() и
и ![]() шатуна 2 и 3 в точку B и D соответственно
(лист 2). При этом, для шатуна 2, точка А считается неподвижной. В этом случае
полученная система будет совершать вращательные движения вокруг условно
неподвижной точки А против часовой стрелки. Следовательно, момент от сил
инерции шатуна 2
шатуна 2 и 3 в точку B и D соответственно
(лист 2). При этом, для шатуна 2, точка А считается неподвижной. В этом случае
полученная система будет совершать вращательные движения вокруг условно
неподвижной точки А против часовой стрелки. Следовательно, момент от сил
инерции шатуна 2 ![]() направлен по направлению
действия часовой стрелки. Определив таким же образом направление действия момента
инерции от шатуна 3
направлен по направлению
действия часовой стрелки. Определив таким же образом направление действия момента
инерции от шатуна 3 ![]() получим, что линия действия
этого момента совпадает с направлением действия часовой стрелки.
получим, что линия действия
этого момента совпадает с направлением действия часовой стрелки.
Нанесем на построенную
кинематическую схему 4 положения внешние нагрузки, определенные выше, а также
силы полезного сопротивления (лист 2). Масштабный коэффициент примем ![]() В результате полученная картина будет
являться расчетной схемой для данной группы звеньев механизма двухтактного ДВС
с передачей к цилиндру для сжатия горючей смеси.
В результате полученная картина будет
являться расчетной схемой для данной группы звеньев механизма двухтактного ДВС
с передачей к цилиндру для сжатия горючей смеси.
3.2 Метод кинетостатики для одного положения кривошипа.
Из полученной расчетной модели
выделим структурную группу Асура, звенья 3 – 5. Отброшенные звенья заменим их
реакциями. Вектор изображающий реакцию стойки 0 на ползун 5 ![]() направлен перпендикулярно поверхности
соприкосновения ползуна 5 и стойки 0 в точки D.
Направление вектора изображающего реакцию шатуна 2 на шатун 3
направлен перпендикулярно поверхности
соприкосновения ползуна 5 и стойки 0 в точки D.
Направление вектора изображающего реакцию шатуна 2 на шатун 3 ![]() нам неизвестно, поэтому разобьем вектор на
перпендикулярную
нам неизвестно, поэтому разобьем вектор на
перпендикулярную ![]() и нормальную
и нормальную ![]() составляющую в точке С (лист 2).
составляющую в точке С (лист 2).
Запишем уравнение равновесии для полученной схемы:
![]() , (3.2.1)
, (3.2.1)
Уравнение (3.2.1) содержит 3
неизвестных ![]() следовательно его статическая
неопределимость равна 2.
следовательно его статическая
неопределимость равна 2.
С целью раскрытия статической
неопределимости найдем модуль реакции ![]() . Для
этого запишем сумму всех моментов относительно точки D
. Для
этого запишем сумму всех моментов относительно точки D ![]() ;
;
![]() , (3.2.2)
, (3.2.2)
где ![]() ,
, ![]() - плечо для сил
- плечо для сил ![]() и
и
![]() соответственно. Получим:
соответственно. Получим:
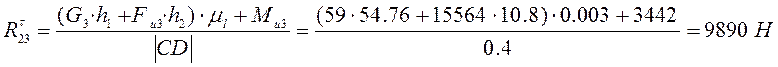
В результате проведенных
вычислений уравнение (3.2.1) содержит 2 неизвестных ![]() ,
следовательно, статическая неопределимость раскрыта полностью. Определение оставшихся
неизвестных выполним с помощью плана сил.
,
следовательно, статическая неопределимость раскрыта полностью. Определение оставшихся
неизвестных выполним с помощью плана сил.
Масштабный коэффициент плана сил:
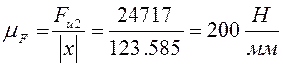 , (3.2.3)
, (3.2.3)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.