Точка пересечения этих прямых позволит найти величины
и направление векторов ![]() и
и ![]() Измерив длины отрезков
Измерив длины отрезков ![]() и
и ![]() и умножив их на масштабный коэффициент
ускорений, в котором строится план ускорений, получим истинные значения
и умножив их на масштабный коэффициент
ускорений, в котором строится план ускорений, получим истинные значения ![]() и
и ![]()
![]()
![]()
Найдём угловое ускорение второго звена, зная тангенциальное
ускорение ![]() точки B:
точки B:
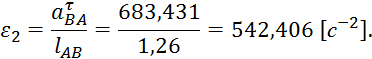
Направлено ![]() в ту же сторону, куда и
в ту же сторону, куда и ![]()
Найдём угловое ускорение третьего звена, зная
тангенциальное ускорение ![]() точки B:
точки B:
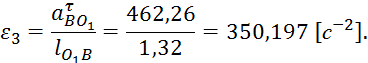
Направлено ![]() в ту же сторону,
куда и
в ту же сторону,
куда и ![]() .
.
Найдём угловое ускорение четвёртого звена, зная
тангенциальное ускорение ![]() точки D:
точки D:
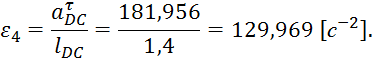
Направлено ![]() в ту же сторону, куда и
в ту же сторону, куда и ![]() .
.
Мы нашли значение и направления линейных ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() и угловых
и угловых ![]() ,
, ![]() ,
, ![]() ускорений для
второго положения механизма.
ускорений для
второго положения механизма.
Строим планы ускорений для оставшихся положений механизма. Вычисляем истинные величины линейных и угловых ускорений для всех положений механизма и сводим их в таблицу
Таблица 3 – Угловые и линейные ускорения точек звеньев для двенадцати положений механизма
|
Номер положе-ния механизма |
Ускорения точек, |
Угловые ускорения
звеньев, |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,12 |
414,1 |
242,522 |
138,043 |
73,668 |
0 |
242,522 |
231,499 |
245,611 |
0 |
23,181 |
58,467 |
183,729 |
16,558 |
|
1 |
414,1 |
366,826 |
75,269 |
342,85 |
22,038 |
366,164 |
350,155 |
345,508 |
0,062 |
7,156 |
272,103 |
277,397 |
5,111 |
|
2 |
414,1 |
476,613 |
1,188 |
683,431 |
116,115 |
462,26 |
454,947 |
316,372 |
0,738 |
181,956 |
542,406 |
350,197 |
129,969 |
|
3 |
414,1 |
365,071 |
110,27 |
771,203 |
276,383 |
238,513 |
348,473 |
173,558 |
30,167 |
450,052 |
612,066 |
180,692 |
321,466 |
|
4 |
414,1 |
598,101 |
303,184 |
68,169 |
208,235 |
560,675 |
570,911 |
611,849 |
96,609 |
21,831 |
54,102 |
424,754 |
15,594 |
|
5 |
414,1 |
787,386 |
191,743 |
421,686 |
12,295 |
787,237 |
751,6 |
12,928 |
11,3 |
741,048 |
334,671 |
596,392 |
529,32 |
|
6 |
414,1 |
473,548 |
50,694 |
393,279 |
41,662 |
471,71 |
452,023 |
138,119 |
33,958 |
338,527 |
312,126 |
357,356 |
241,805 |
|
7 |
414,1 |
216,193 |
4,345 |
317,739 |
112,455 |
184,647 |
206,363 |
290,889 |
48,668 |
70,298 |
252,174 |
139,884 |
50,213 |
|
8 |
414,1 |
138,5 |
5,187 |
275,791 |
137,064 |
19,661 |
132,206 |
177,864 |
23,1 |
199,795 |
218,882 |
14,895 |
142,711 |
|
9 |
414,1 |
188,432 |
38,379 |
250,017 |
107,396 |
154,832 |
179,868 |
16,092 |
4,376 |
168,671 |
198,426 |
117,297 |
120,479 |
|
10 |
414,1 |
235,118 |
91,357 |
194,453 |
56,459 |
228,244 |
224,434 |
163,205 |
0,104 |
81,023 |
154,328 |
172,912 |
57,874 |
|
11 |
414,1 |
135,328 |
136,859 |
279,575 |
15,62 |
134,417 |
129,174 |
102,937 |
14,435 |
23,256 |
221,885 |
101,831 |
16,611 |
|
13 |
414,1 |
355,157 |
138,043 |
223,448 |
0 |
355,157 |
339,015 |
23,67 |
0 |
358,138 |
177,34 |
269,058 |
255,813 |
Силовой анализ будем проводить кинетостатическим методом (в число заданных сил при расчёте входят силы инерции), при этом будем определять реакции в связях кинематических пар и уравновешивающую силу (уравновешивающий момент).
Построим в заданном масштабном коэффициенте длин второе
положение механизма в масштабном коэффициенте длин ![]() Построим для него план ускорений.
Построим для него план ускорений.
Рассчитаем силы, действующие на звенья.
Сила
тяжести ![]() равна:
равна:
![]()
где ![]() – масса звена i-го
звена;
– масса звена i-го
звена;
![]() –
ускорение свободного падения, равное
–
ускорение свободного падения, равное ![]()
Масса
звена ![]() равна:
равна:
![]()
где ![]() – удельная масса i-го
звена;
– удельная масса i-го
звена;
![]() – длина i-го
звена.
– длина i-го
звена.
Для
кривошипов: ![]()
Для
шатунов:![]()
Для
коромысел: ![]()
Масса
ползуна: ![]() где
где ![]() – масса шатуна к которому прикреплён
ползун.
– масса шатуна к которому прикреплён
ползун.
Значит:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Центр
масс кривошипа лежит на оси вращения кривошипа, шатуна – на середине его длины,
коромысла– на звене ![]() на расстоянии 0,03м
от точки
на расстоянии 0,03м
от точки ![]() .
.
Откладываем
вектора сил тяжести ![]()
![]()
![]()
![]()
![]() на положении механизма соответственно от
точек
на положении механизма соответственно от
точек ![]()
![]()
![]()
![]()
![]()
Определим силы инерции звеньев.
Сила
инерции ![]() может быть определена по формуле:
может быть определена по формуле:
![]()
где ![]() – вектор силы инерции i-го
звена;
– вектор силы инерции i-го
звена;
![]() – масса i-го
звена;
– масса i-го
звена;
![]() – вектор полного ускорения центра масс
– вектор полного ускорения центра масс ![]() i-го звена.
i-го звена.
Как
видно из формулы ![]() и равна по величине
и равна по величине
![]() .
.
Момент
![]() пары сил инерции направлен противоположно
угловому ускорению
пары сил инерции направлен противоположно
угловому ускорению ![]() и может быть определён по формуле:
и может быть определён по формуле:
![]()
где ![]() – момент инерции звена относительно оси,
проходящей через центр масс
– момент инерции звена относительно оси,
проходящей через центр масс ![]() и перпендикулярной к плоскости движения
звена;
и перпендикулярной к плоскости движения
звена;
![]() – угловое ускорение звена.
– угловое ускорение звена.
Момент инерции шатунов определится по формуле:
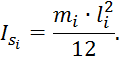
Определим
из плана ускорений ускорения ![]()
![]()
![]()
![]()
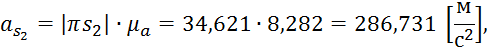
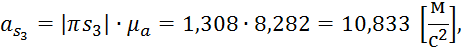
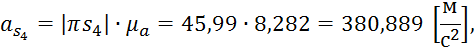
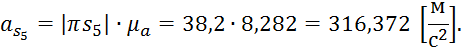
Рассчитаем силы инерции:
![]()
![]()
![]()
![]()
Построим на чертеже положений механизма силы инерции.
Рассчитаем моменты инерции второго, третьего и четвёртого звеньев:
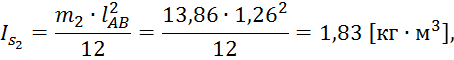
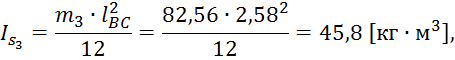
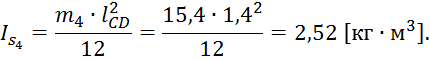
Рассчитаем моменты пар сил инерции для второго, третьего и четвёртого звеньев:
![]()
![]()
![]()
Покажем на чертеже моменты пар сил инерции второго, третьего и четвёртого звеньев и данные силы полезного сопротивления.
Теперь необходимо сделать расчленение механизма. Силовой расчёт начинают с наиболее удалённой от первичного механизма структурной группы Ассура.
Рассмотрим структурную группу Ассура 4-5. Запишем уравнение кинетостатического равновесия:
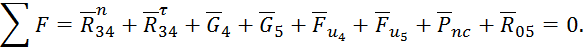
Здесь ![]() и
и ![]() – силы реакций, приложенные соответственно
к звеньям 5 и 4 со стороны звеньев, образующих кинематические пары.
– силы реакций, приложенные соответственно
к звеньям 5 и 4 со стороны звеньев, образующих кинематические пары.
Запишем уравнение суммы моментов относительно точки D:
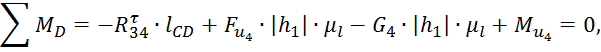
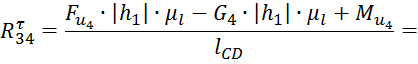
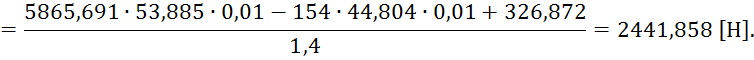
![]()
Таким образом в уравнении осталось две неизвестных силы, их можно определить составлением векторного силового многоугольника. Для его составления воспользуемся выражением.
Масштабный коэффициент
сил ![]() :
:
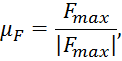
где ![]() – истинное значение известной максимальной
силы, входящей в уравнение;
– истинное значение известной максимальной
силы, входящей в уравнение;
![]() – длина этой силы на плане скоростей.
– длина этой силы на плане скоростей.
Примем масштабный коэффициент сил:
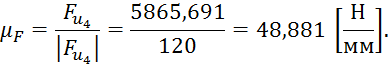
Строим многоугольник сил, для этого, сначала рассчитаем длины векторов сил на плане сил:
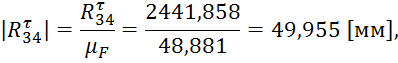
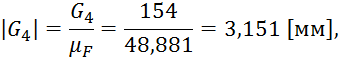
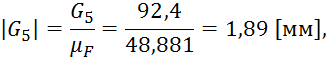
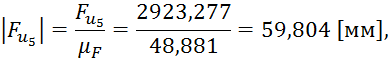
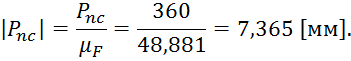
Из произвольной
точки строим вектор ![]() , потом из конца этого вектора вектор
, потом из конца этого вектора вектор ![]() и так далее. Завершают многоугольник сил,
проводя из начала вектора
и так далее. Завершают многоугольник сил,
проводя из начала вектора ![]() прямую параллельную CD,
а из конца вектора
прямую параллельную CD,
а из конца вектора ![]() прямую перпендикулярную DO. Точка пересечения этих прямых позволяет построить
силы
прямую перпендикулярную DO. Точка пересечения этих прямых позволяет построить
силы ![]() и
и ![]() на плане сил и определить их истинное
значение.
на плане сил и определить их истинное
значение.
![]()
![]()
![]()
Рассмотрим структурную группу Ассура 4-5. Запишем уравнение кинетостатического равновесия:
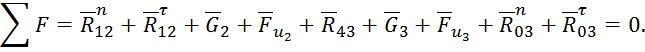
Здесь
![]() и
и ![]() – силы реакций, приложенные к звену 3 со
стороны стойки,
– силы реакций, приложенные к звену 3 со
стороны стойки, ![]() – силы реакций, приложенные к звену 2 со стороны
звена
– силы реакций, приложенные к звену 2 со стороны
звена
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.