Кулачковые механизмы. Определение значения угловых и линейных скоростей

Кулачковые механизмы.

Кулачковые механизмы- это механизмы с высшими кинематическими парами, обладающие возможностью точных выстоев выходного звена.

Дано: , , , , , , .

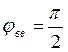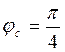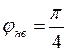Произведем структурный анализ.

Для определения подвижности воспользуемся формулой Чебушева:

, где n=3

,  

,   

где - местная подвижность, образованная роликом и звеном

Зададим масштабный коэффициент оси угла поворота:

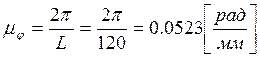
- Период работы кулачка, разобьем его на фазовые углы: , , ,

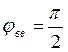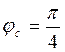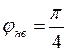
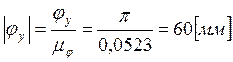
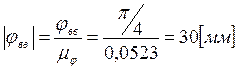
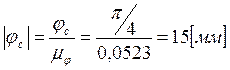
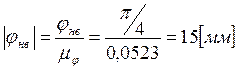
Выполним расчет диаграммы пути S:

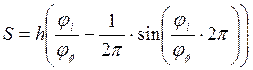
где  то есть фазовый угол соответствующей фазы, 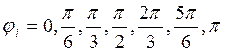. – текущее значение фазового угла

Для остальных положений расчет производится аналогично.

Далее выполним расчет диаграммы аналога скорости  используя следующую формулу:

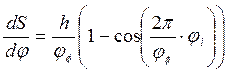
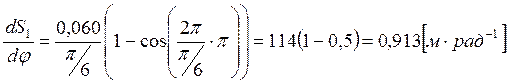
Для остальных положений расчет производится аналогично.

Далее выполним расчет диаграммы аналога ускорения  используя следующую формулу:

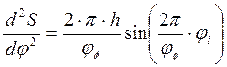
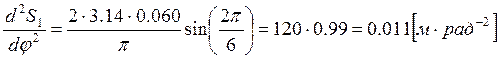
Для остальных положений расчет производится аналогично.

После проведенных расчетов занесем найденные величины в таблицу:

	S (м)
0	0	0	0
1	0,0011	0,953	0,011
2	0,0074	0,960	0,012
3	0,0086	0,966	0,006
4	0,0089	0,977	0,013
5	0,0096	0,980	0,010
6	0,010	0	0
7	0,010	0	0
8	0,0096	0,980	0,006
9	0,0089	0,977	0,0063
10	0,0086	0,966	0,011
11	0,0074	0,960	0,08
12	0,0011	0,953	0,044
13	0	0	0
14	0	0	0

Теперь для построения диаграмм необходимо задать масштабные коэффициенты пути, аналога скорости и аналога ускорения:

 

;

;

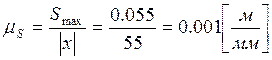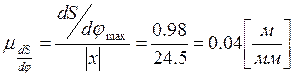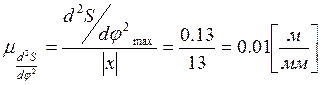
Переведем все величины для каждого положения в масштабные коэффициенты и занесем полученные результаты в таблицу:

	S (м)
0	0	0	0
1	1,1	22,8	11
2	7,4	23,8	12
3	15,5	24,25	6
4	22,4	24,5	-13
5	30,5	24,9	-10
6	38,4	0	0
7	38,5	0	0
8	30,5	27,76	-6,3
9	22,4	27,2	11
10	15,5	26,5	8
11	7,4	24,4	4
12	1,1	22,8	8
13	0	0	0
14	0	0	0

После определения данных величин можно преступать к построению диаграмм S; ; .

Далее после построения диаграмм строим исходный контур из которого нам становится известным  а следовательно можем приступить к построению теоретического контура кулачка. Так же по исходному контуру нам необходимо найти углы давления для каждой точки. Выполним вышеперечисленные действия и получим:

;

Тогда радиус ролика будет:

Для нахождения углов давления необходимо: через каждую точку на исходном контуре провести перпендикуляр к оси ; затем необходимо каждую из этих точек соединить с центром вращения кулачка ; потом нужно измерить угол между двумя этими линиями таким образом мы получим углы давления для каждого положения. найденные величины сведем в таблицу:

Точки
0	0	30
1	20	30
2	23	30
3	25	30
4	15	30
5	18	30
6	0	30
7	0	30
8	25	30
9	23	30
10	25	30
11	26	30
12	23	30
13	0	30
14	0	30

Ни одно из значений угла давления не превышает допустимого

следовательно условие  выполняется.

Сложные зубчатые механизмы.

Дано: ; ; .

В данном разделе курсового проекта представлена схема сложного зубчатого механизма. Который условно можно разделить на планетарный зубчатый механизм и простую зубчатую передачую

Проводим структурный анализ.

 , где n = 5

P1(0-1;0-2;03;н-4;0-7)=5,   P2(1-2;3-4;4-5;6-7)=4

Метрический синтез.

U13=5;  U67=2,5;  Uн4=8,5

Z1min=20;   Z2=85;  Z6=34.

Используем формулу Виллиcа: 

Вычисляем числа зубьев для каждого варианта составим таблицу.

Условие соостности:

Z5=Z4=Z′4=Z6

A+B=C+D

A(A+B)=b(C+D)

a= C+D; b=A+B.

Z5=aA

Z4=aB

Z′4=bC

Z6=bD

Условие отсутствия интерференции:

Условие соседства:

Условие сборки:

Условие сборки подходит только для 3 варианта чисел зубьев колёс. Этот вариант отвечает всем 5 условиям передаточное число последнего ряда.

Определим делительные диаметры всех колёс: d = mz1

d1= m∙z1=3∙20=60мм=0,06м

d2= m∙z2=3∙34=102мм=0,102м

d3= m∙z3=3∙27= 81мм=0,081м

d4= m∙z4=3∙70=210мм=0,21м

d′4= m∙z′4=3∙66=198мм=0,198м

d5= m∙z5=3∙40=120мм=0,12м

d6= m∙z6=3∙44= 132мм=0,132м

d7= m∙z7=3∙88=264мм=0,264м

Переводим в масштабный коэффицент:

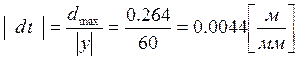
│d1│	│d2│	│d3│	│d4│	│d′4│	│d5│	│d6│	│d7│	VD	VF	VE	VB
19	69	20	80	75	45	50	100	105	20	10	53

Определяем значение угловых и линейных скоростей характерных точек механизма: =29,3c

VA= ∙ =

; 

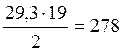
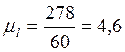
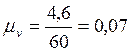
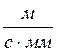
После  построения плана измеряем отрезки, отображающие действительные величины скоростей и определяем V02 и Vc:

Vc=│CC1│∙ = 2∙0,07=0,14

V02=│OO1│∙=5∙0,07=0,35

Для определения угловых скоростей необходимо на плане линейных скоростей построить годографы, посредствам которых строиться план угловых скоростей.

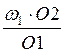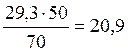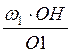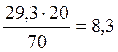======,   где = =с

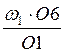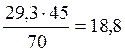=с,   = =с

=′ ,  =′

Список используемых источников.

1)  Конспект лекций.

2)  Н.И. Левитский,  “Теория механизмов и машин” 1979г.-376 стр.

3)  С.А.Попов,” Курсовое проектирование по теории механизмов и машин”

1936г.- 295 стр.