где ![]() – модуль силы инерции шатуна 3 ,
Н;
– модуль силы инерции шатуна 3 ,
Н; ![]() – произвольно выбранный отрезок,
изображающий на плане сил вектор силы инерции шатуна 3.
– произвольно выбранный отрезок,
изображающий на плане сил вектор силы инерции шатуна 3.
Переведем в масштабный коэффициент остальные силы:
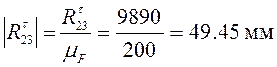 ;
;
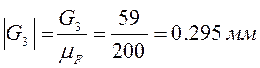 ;
;
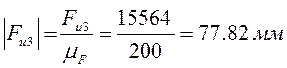 ;
;
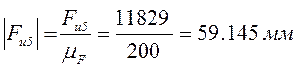 ;
;
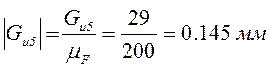 ;
;
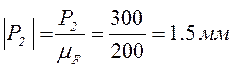 .
.
По полученным величинам строим
план сил в масштабном коэффициенте 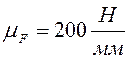 (лист 2).
(лист 2).
Модули реакций:
![]() ;
;
![]() ;
;
![]() ;
;
Рассмотрим следующую структурную
группу Асура, звенья 4 – 2. Отброшенные звенья заменим их реакциями. Вектор изображающий
реакцию стойки 0 на ползун 4 ![]() направлен перпендикулярно
поверхности соприкосновения ползуна 4 и стойки 0 в точки В. Направление
вектора изображающего реакцию кривошипа 1 на шатун 2
направлен перпендикулярно
поверхности соприкосновения ползуна 4 и стойки 0 в точки В. Направление
вектора изображающего реакцию кривошипа 1 на шатун 2 ![]() нам
неизвестно, поэтому разобьем вектор на перпендикулярную
нам
неизвестно, поэтому разобьем вектор на перпендикулярную ![]() и
нормальную
и
нормальную ![]() составляющую в точке А (лист 2).Вектор
силы реакции шатуна 3 на шатун 2
составляющую в точке А (лист 2).Вектор
силы реакции шатуна 3 на шатун 2 ![]() равен вектору силы
реакции шатуна 2 на шатун 3
равен вектору силы
реакции шатуна 2 на шатун 3 ![]() , но противоположен по направлению.
, но противоположен по направлению.
Запишем уравнение равновесия для полученной схемы:
![]() , (3.2.4)
, (3.2.4)
Уравнение (3.2.1) содержит 3
неизвестных ![]() следовательно его статическая
неопределимость равна 2.
следовательно его статическая
неопределимость равна 2.
С целью раскрытия статической
неопределимости найдем модуль реакции ![]() . Для
этого запишем сумму всех моментов относительно точки В
. Для
этого запишем сумму всех моментов относительно точки В ![]() ;
;
![]() , (3.2.5)
, (3.2.5)
где ![]() ,
, ![]() - плечо для сил
- плечо для сил ![]() и
и
![]() соответственно. Получим:
соответственно. Получим:
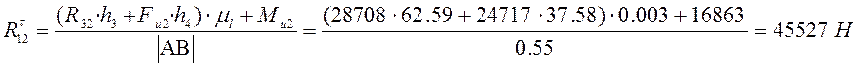
В результате проведенных
вычислений уравнение (3.2.1) содержит 2 неизвестных ![]() ,
следовательно, статическая неопределимость раскрыта полностью. Определение
оставшихся неизвестных выполним с помощью плана сил.
,
следовательно, статическая неопределимость раскрыта полностью. Определение
оставшихся неизвестных выполним с помощью плана сил.
Масштабный коэффициент плана сил:
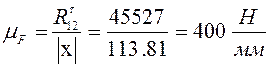 , (3.2.6)
, (3.2.6)
где ![]() – модуль реакции кривошипа 1 на
шатун 2 , Н;
– модуль реакции кривошипа 1 на
шатун 2 , Н; ![]() – произвольно выбранный отрезок,
изображающий на плане сил вектор реакции кривошипа 1 на шатун 2.
– произвольно выбранный отрезок,
изображающий на плане сил вектор реакции кривошипа 1 на шатун 2.
Переведем в масштабный коэффициент все силы:
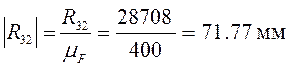 ;
;
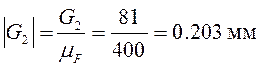 ;
;
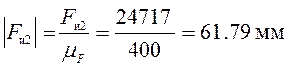 ;
;
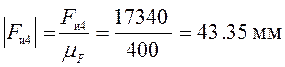 ;
;
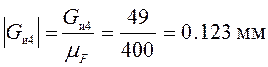 ;
;
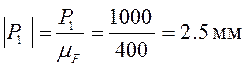 .
.
По полученным величинам строим
план сил в масштабном коэффициенте 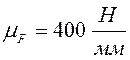 (лист 2).
(лист 2).
Модули реакций:
![]() ;
;
![]() ;
;
![]() ;
;
Рассмотрим первичный механизм,
звенья 1 – 0. Отброшенные звенья заменим их реакциями. Направление вектора
изображающего реакцию стойки 0 на кривошип 1 ![]() нам
неизвестно, поэтому разобьем вектор на перпендикулярную
нам
неизвестно, поэтому разобьем вектор на перпендикулярную ![]() и
нормальную
и
нормальную ![]() составляющую в точке О (лист 2).Вектор
силы реакции шатуна 2 на кривошип 1
составляющую в точке О (лист 2).Вектор
силы реакции шатуна 2 на кривошип 1 ![]() равен по модулю вектору
силы реакции кривошипа 1 на шатун 2
равен по модулю вектору
силы реакции кривошипа 1 на шатун 2 ![]() , но противоположен по
направлению.
, но противоположен по
направлению.
Запишем уравнение равновесия для полученной схемы:
![]() , (3.2.7)
, (3.2.7)
Уравнение (3.2.1) содержит 3
неизвестных ![]() следовательно его статическая
неопределимость равна 2.
следовательно его статическая
неопределимость равна 2.
С целью раскрытия статической
неопределимости найдем модуль реакции ![]() . Для
этого запишем сумму всех моментов относительно точки А
. Для
этого запишем сумму всех моментов относительно точки А ![]() ;
;
![]() , (3.2.8)
, (3.2.8)
где ![]() ,
, ![]() - плечо для сил
- плечо для сил ![]() и
и
![]() соответственно. Получим:
соответственно. Получим:

В результате проведенных
вычислений уравнение (3.2.1) содержит 2 неизвестных ![]() ,
следовательно, статическая неопределимость раскрыта полностью. Определение
оставшихся неизвестных выполним с помощью плана сил.
,
следовательно, статическая неопределимость раскрыта полностью. Определение
оставшихся неизвестных выполним с помощью плана сил.
Масштабный коэффициент плана сил:
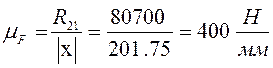 , (3.2.9)
, (3.2.9)
где ![]() – модуль реакции шатуна 2 на кривошип
1, Н;
– модуль реакции шатуна 2 на кривошип
1, Н; ![]() – произвольно выбранный отрезок,
изображающий на плане сил вектор реакции шатуна 2 на кривошип 1.
– произвольно выбранный отрезок,
изображающий на плане сил вектор реакции шатуна 2 на кривошип 1.
Переведем в масштабный коэффициент все силы:
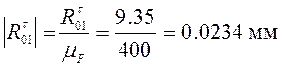 ;
;
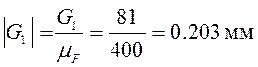 ;
;
По полученным величинам строим
план сил в масштабном коэффициенте 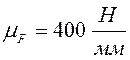 (лист 2).
(лист 2).
Модули реакций:
![]() ;
;
![]() ;
;
![]() ;
;
Момент управляющего воздействия:
![]() .
.
3.3 Теория Жуковского для 4 положения ведущего звена.
Определим управляющей
воздействие механизма с помощью теоремы Жуковского: если механизм под действием
системы сил находится в равновесии, то в равновесии находится и повернутый на ![]() план скоростей, рассматриваемый как
жесткий рычаг, вращающийся вокруг полюса плана скоростей и нагруженный той же
системой сил, приложенных в одноименных точках плана.
план скоростей, рассматриваемый как
жесткий рычаг, вращающийся вокруг полюса плана скоростей и нагруженный той же
системой сил, приложенных в одноименных точках плана.
Согласно теореме Жуковского
нанесем на повернутый на ![]() по часовой стрелки план
скоростей 4 положения механизма систему сил, приложенную в соответствующих точках.
по часовой стрелки план
скоростей 4 положения механизма систему сил, приложенную в соответствующих точках.
Моменты инерции ![]() , действующие на звенья, заменим парой сил
, действующие на звенья, заменим парой сил ![]() и
и ![]() , каждая
из которых равна:
, каждая
из которых равна:
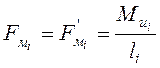 ; (3.3.1)
; (3.3.1)
Определим значение пары сил действующие на шатун 2 и 3:
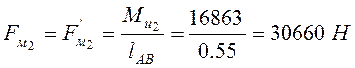 .
.
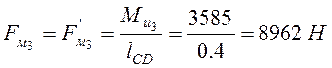
Нанесем на план скоростей
управляющее воздействие ![]() . Теперь план скоростей
нагруженный системой сил находится в квазистатическом равновесии. Это позволит
нам определить значение управляющего воздействия, воспользовавшись условием
равновесия
. Теперь план скоростей
нагруженный системой сил находится в квазистатическом равновесии. Это позволит
нам определить значение управляющего воздействия, воспользовавшись условием
равновесия ![]() , получим:
, получим:
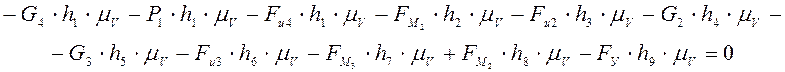
В итоге получим:
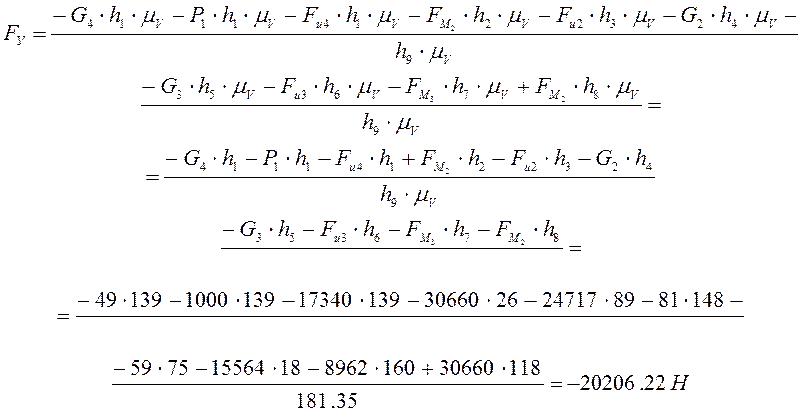
Тогда момент управляющего воздействия:
![]() .
.
Погрешность расчетов: пересчитать
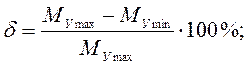
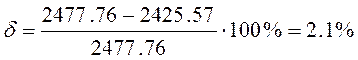
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.