ФВ=
BScosa = BScos(![]() ), (82)
), (82)
где S = а2- площадь рамки.
Подставим уравнение (82) в формулу (80) и найдем закон изменения ЭДС с течением времени:
E 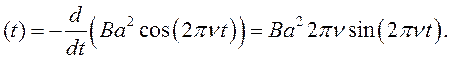 (83)
(83)
Подставим данные задачи в выражение (83):
E ![]() (В).
(В).
Максимальное значение ЭДС
найдем из закона ее изменения (при cos(![]() ) = 1):
) = 1):
E ![]() (84)
(84)
E ![]() В.
В.
Ответ: E ![]() В;
В; ![]() В.
В.
Задача 11. Круглая рамка из 100 витков алюминиевой проволоки сечением 3 мм2 помещена в магнитное поле, индукция которого меняется по закону: B = B0sinwt, где В0 = 0,1 Тл, w = 6 рад/с. Радиус витка рамки равен 10 см. Найти законы изменения ЭДС индукции и силы тока в рамке с течением времени, а также их максимальные значения. Линии магнитной индукции совпадают с нормалью к рамке (рис. 21).
Дано: N = 100; Scеч = 3 мм2; B = B0sinwt; B0 = 0,1 Тл; w = 6 рад/с; r = 10 см; a = 0; rAl = 2,8×10-8 Ом×м |
СИ 3×10-6 м2 0,1 м |
При изменении магнитного поля будет меняться магнитный поток, пронизывающий рамку. Вследствие этого в рамке возникает ЭДС индукции, которую можно найти по закону Фарадея-Ленца: E |
|
E (t) – ? i(t) – ? E max– ? imax - ? |
Закон изменения потокосцепления от времени в рамке имеет следующий вид:
![]() (86)
(86)
где Sp - площадь рамки, Sp = pr2.
Подставим формулу (86) в уравнение (85) и найдем закон изменения ЭДС с течением времени:
E 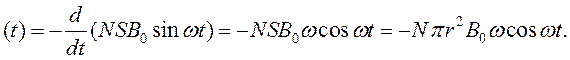 (87)
(87)
Знак «-» в формуле (85) означает то, что
действие сторонних сил направлено против положительного направления обхода
контура, которое связано с вектором магнитной индукции ![]() правилом
правого винта.
правилом
правого винта.
Подставим данные задачи в формулу (87):
E (t) = -100×3,14×10-2×0,1×6 cos6t = -1,9 cos6t (B).
Максимальное значение ЭДС найдем из закона ее изменения:
E max = Npr2B0w ; (88)
E max = 1,9 B.
Для нахождения закона изменения индукционного тока воспользуемся законом Ома для замкнутой цепи:
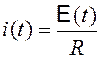 , (89)
, (89)
где R - сопротивление рамки,
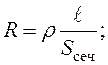 (90)
(90)
![]() (91)
(91)
здесь ℓ - длина проводника.
В результате преобразований формула (90) примет вид:
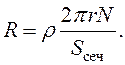 (92)
(92)
Подставим формулы (88) и (92) в уравнение (89):
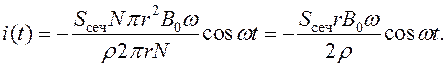 (93)
(93)
Подставим в уравнение (93) данные задачи:
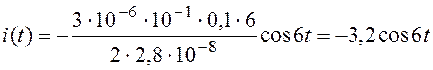 (A).
(A).
Максимальное значение силы индукционного тока найдем из закона его изменения:
imax = 3,2 A.
Ответ: E (t) = -1,9 cos6t B; ![]() А; E max = 1,9 B; imax = 3,2
мкА.
А; E max = 1,9 B; imax = 3,2
мкА.
Задача 12. Квадратная рамка, состоящая из одного витка, со стороной 5 см и сопротивлением 0,03 Ом находится в однородном магнитном поле с индукцией 30 мТл. Плоскость рамки перпендикулярна линиям индукции. Какой за-
ряд протечет по рамке, если ее повернуть так, чтобы угол между нормалью к рамке и линиями индукции стал равен 60°?
Дано: a = 5 см; R = 0,03 Ом;
a2 = 60° |
СИ 5×10-2 м |
Решение.
|
|
q– ? |
При повороте рамки меняется магнитный поток, который ее пронизывает. По рамке потечет индукционный ток i, который можно найти по закону Ома:
![]()
![]()
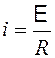 , (94)
, (94)
где R - сопротивление рамки.
Для замкнутой цепи ЭДС индукции E вычисляется по закону Фарадея-Ленца:
E 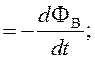 (95)
(95)
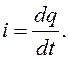 (96)
(96)
Заряд q, который протечет по контуру, определим через силу тока:
![]()
![]() = i =
= i = 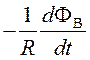 ; (97)
; (97)
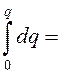
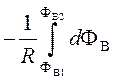 ;
(98)
;
(98)
![]()
![]() =
= 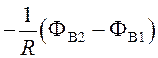 . (99)
. (99)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.