Физика \ Физика

Методические указания для самостоятельной работы студентов при изучении раздела физики «Электромагнетизм», страница 7

Квадратная рамка с током I2 находится в неоднородном магнитном поле прямого тока. Индукцию магнитного поля бесконечно длинного проводника с током определяем по формуле:

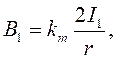                                                (69)

где r - расстояние от прямого тока до рассматриваемой точки.

Вектор  во всех точках рамки перпендикулярен плоскости рамки.

Работа внешних сил при повороте рамки равна работе сил поля, взятой с обратным знаком:

                                  (70)

где  и  - магнитные потоки, пронизывающие рамку до и после поворота.

Вследствие неоднородности поля прямого тока магнитный поток рассчитываем по формуле:

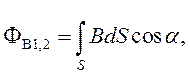                                           (71)

где a - угол между направлением магнитной индукции и правовинтовой нормалью к рамке.

Для расчета потока выберем элементарную площадку dS (изображена на рис. 19 в виде заштрихованного прямоугольника), в пределах которой величину индукции В1 можно считать постоянной:

                                                  (72)

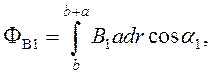                                         (73)

где a1 =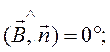

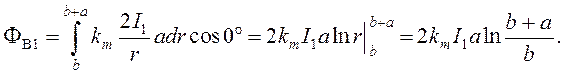            (74)

При повороте рамки изменяется угол между нормалью к рамке и направлением магнитной индукции, а также расстояние от провода до рамки. Тогда магнитный поток вычисляется по формуле:

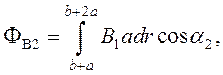                                         (75)

где a2 = a1 + j = p ;

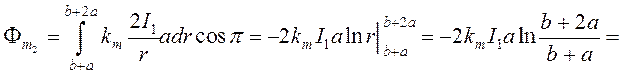
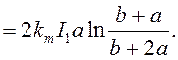                                           (76)

Подставив выражения (74) и (76) для потоков  и  в формулу (70), получим:

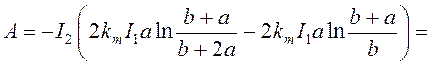
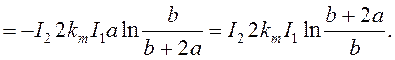                           (77)


Подставив данные задачи в формулу (77), рассчитаем работу, которую нужно выполнить при повороте рамки:

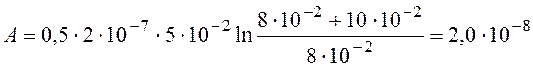 (Дж).

Ответ: А = 20 нДж.

4. ЯВЛЕНИЕ  ЭЛЕКТРОМАГНИТНОЙ  ИНДУКЦИИ.

ЗАКОН  ФАРАДЕЯ-ЛЕНЦА

Явление электромагнитной индукции заключается в том, что во всяком проводящем замкнутом контуре  при изменении магнитного потока, проходящего через поверхность, ограниченную этим контуром, возникает электрический ток, называемый индукционным. Это свидетельствует о возникновении в контуре электродвижущей силы E, которая определяется по закону Фарадея-Ленца:

E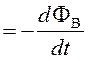.                                                 (78)

Если имеется несколько витков, то электродвижущую силу можно найти по формуле:

E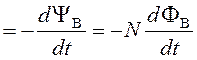,                                        (79)

где Y– потокосцепление, Y = NФВ;

 N - число витков.

При решении задач этого раздела следует обратить внимание на то, что значение электродвижущей силы не зависит от причины изменения магнитного потока. Величина магнитного потока ФВ может меняться по разным причинам, например, если изменяется

1) магнитная индукция;

2) площадь, охватываемая контуром;

3) угол между нормалью к контуру и вектором магнитной индукции (при ориентации контура в магнитном поле).

ЭДС индукции может возникать в проводнике, который двигается или вращается в магнитном поле, пересекая его силовые линии.

Примеры решения задач

Задача 10. Квадратная рамка со стороной 5 см равномерно вращается с частотой 5 об/с в однородном магнитном поле с индукцией 30 мТл. Определить закон изменения ЭДС индукции и максимальное значение ЭДС. Ось вращения лежит в плоскости рамки и перпендикулярна линиям индукции.


Дано:

a = 5 см;

B = 30 мТл;

n = 5 об/с

СИ

0,05 м

0,03 Тл

Решение.

При вращении рамки будет изменяться угол a между нормалью к контуру и вектором магнитной индукции, следовательно, будет меняться и магнитный поток, пронизывающий рамку. Вследствие этого по рамке потечет индукционный ток  и  возникнет

E– ?

Emax– ?

ЭДС индукции, которую можно найти по закону Фарадея-Ленца:

E = 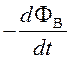.                                               (80)

При равномерном вращении угол a будет изменяться по закону:

.                                               (81)

Тогда, так как поле однородное, закон изменения магнитного потока через рамку имеет следующий вид:

Скачать файл