Методические указания для самостоятельной работы студентов при изучении раздела физики «Электромагнетизм», страница 2

Магнитное поле нити с током в форме кольца показано на рис. 4. Линии индукции поля изображены в плоскости, перпендикулярной витку и проходящей через ось симметрии.

Направление вектора магнитной индукции на оси ОО¢, в частности в центре витка с током (рис. 5) можно определить также по правилу буравчика: если буравчик с правой резьбой вращать по направлению тока, то поступательное движение буравчика покажет направление .

Магнитное поле соленоида изображено на рис. 6. Направление вектора магнитной индукции на оси соленоида определяется так же, как и в случае кругового тока.

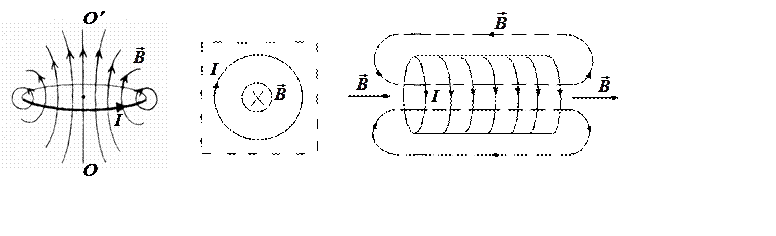
Рис. 4                          Рис. 5                                   Рис. 6

При решении задач этого раздела надо иметь в виду, что для магнитного поля в вакууме и воздухе, как и для электрического, справедлив принцип суперпозиции полей: если имеется несколько токов, каждый из которых создает магнитное поле, то магнитные поля не искажают друг друга, а магнитная индукция результирующего поля равна векторной сумме магнитных индукций полей, созданных каждым током в отдельности:

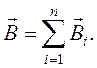                                                   (1)

Для записи векторного уравнения (1) в скалярной форме выбирают координатные оси х, у, zи находят проекции вектора на эти оси:

в_х = в_1х + в_2х + ... + в_nх;(2)

В_у=В_1у + В_2у + ... + В_ny;(3)

в_z = в_1z + в_2z + ... + в_nz.(4)

При решении задач на принцип суперпозиции следует отметить, что круговые витки с током, перпендикулярные плоскости рисунка, принято изображать следующим образом: сторона витка, на которой ставится стрелка, указывающая направление тока, должна быть ближайшей «к нам» (см. рис. 3).

Примеры решения задач

Задача 1. Два бесконечно длинных параллельных проводника с токами I₁ и I₂ расположены так, как показано на рис. 7. Найти величину магнитной индукции поля в точке А, расположенной посередине между проводами, если  I₁ = 4 А,  I₂ = 2 А,  а = 10 см

Запишем принцип суперпозиции в векторном виде:

 =  + .                                                    (5)

Выбрав координатную ось х, направленную вниз, запишем выражение (5) в проекциях на ось х:

B = B₁-B₂.                                                      (6)

Магнитные индукции В₁ и В₂ бесконечно длинных проводников с током определим по формулам:

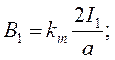                                                    (7)

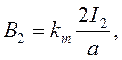                                                    (8)

где k_m - коэффициент пропорциональности, k_m = 10^-7 Н/А².

Подставив формулы (7) и (8) в выражение (6), получим:

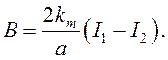                                                  (9)

Вычислим значение магнитной индукции, подставив данные задачи в уравнение (9):

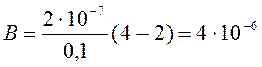 (Тл).

Ответ: В = 4 мкТл.

Задача 2. Два бесконечно длинных проводника с токами I₁ и I₂ и круговой контур с током I₃ расположены так, как показано на рис. 8. Найти магнитную индукцию поля в точке А, если а = 10 см, радиус витка R = 5 см, I₁ = 2 А, I₂ = 4А,  I₃ = 3 А.

Применив правило правого винта, определим  направление векторов индукции ,  и , создаваемых каждым током в отдельности. Для нахождения магнитной индукции  в точке А воспользуемся принципом суперпозиции магнитных полей.

Запишем принцип суперпозиции в векторном виде:

 =  +  + .                                             (10)

Все векторы  , ,  лежат в одной плоскости.