Методические указания для самостоятельной работы студентов при изучении раздела физики «Электромагнетизм», страница 6

При расчете потока вектора магнитной индукции следует обращать внимание на то, какое рассматривается поле: однородное или неоднородное. Для однородного поля

Ф_В = BScosa,                                               (59)

где S – площадь поверхности;

a - угол между нормалью к площадке и магнитной индукцией поля.

Для неоднородного поля Ф_В вычисляется через поверхностный ин-теграл:

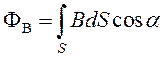.                                            (60)

При перемещении контура с током в магнитном поле совершается работа, которая зависит от приращения магнитного потока через плоскость, ограниченную проводником:

                                   (61)

Примеры решения задач

Задача 7. Круговой контур радиусом 30 см находится в однородном магнитном поле с индукций 0,3 Тл так, что его плоскость составляет угол 60° с линиями магнитной индукции. Найти значение магнитного потока, пронизывающего контур.

Дано: R = 30 см; B = 0,3 Тл; j  = 60°	СИ 0,3 м	Решение.
ФВ– ?

В случае однородного магнитного поля ( = const) поток вектора магнитной индукции

Ф_В = BScosa.                                               (62)

Площадь кругового витка определим по формуле:

S = pR².                                                  (63)

Величину угла a между нормалью  и вектором магнитной индукции найдем из рис. 17:

a = 90° - j  = 90° - 60° = 30°.

Подставим формулу (63) в выражение (62), получим расчетное уравнение:

Ф_В = BpR²cosa.                                             (64)

Рассчитаем поток вектора магнитной индукция, подставив данные задачи в формулу (64):

Ф_В = 0,3p×0,3²cos30° = 0,24 (Вб).

Ответ: Ф_В = 0,24 Вб.

Задача 8. Квадратный контур с током 5 А свободно установился в однородном магнитном поле с индукцией 50 мТл. Сторона квадрата равна 10 см. Поддерживая ток неизменным, контур повернули относительно оси, лежащей в плоскости контура и перпендикулярной линиям индукции, на угол 90°. Определить совершенную при этом работу.

Дано: I = 5 A; B = 50 мТл; a = 10 см; a1 = 0 a2 = 90°	СИ 0,05 Тл 0,1 м	Решение.
А– ?

Квадратная рамка с током I свободно установилась в магнитном поле  (рис. 18, а). Вектор  перпендикулярен плоскости рамки и совпадает по направлению с вектором нормали  (a₁ = 0).

Работа внешних сил при повороте рамки на 90° (рис. 18, б) равна работе сил поля, взятой с противоположным знаком:

А = –А_м.п = ,                                  (65)

где  - магнитные потоки, пронизывающие рамку до и после поворота.

В случае однородного магнитного поля магнитный поток:

Ф_В = BScosa.                                                 (66)

Площадь квадратного контура определим по формуле:

S = а².                                                    (67)

Подставим выражения (66), (67) в уравнение (65) и получим расчетную формулу:

.                                   (68)

Рассчитаем работу внешних сил, подставив данные задачи в формулу (68):

А = -5×0,05×0,1²(cos90° - cos0°) = 2,5×10^-3 (Дж).

Ответ: А = 2,5 мДж.

Задача 9. В одной плоскости с бесконечно длинным прямым проводом, по которому идет ток 5 А, расположена квадратная рамка со стороной а, равной 5 см, обтекаемая током 0,5 А. Ближайшая сторона рамки параллельна прямому току и находится от него на расстоянии b, равном 8 см. Определить работу, которую надо совершить, чтобы повернуть рамку на 180^о вокруг дальней стороны рамки. Токи в проводнике и ближней стороне рамки в начальный момент времени направлены в одну сторону.

Дано: I1 = 5 A; I2 = 0,5 А; a = 5 см; b= 8 см; j  = 180°	СИ 0,05 м 0,08 м	Решение.
А– ?