Физика \ Физика

Методические указания для самостоятельной работы студентов при изучении раздела физики «Электромагнетизм», страница 5

На движущийся заряд в магнитном поле действует сила Лоренца:

.                                            (43)

Направление силы Лоренца определяется по правилу левой руки. Как видно из рис. 15, сила Лоренца перпендикулярна скорости, поэтому она вызывает движение a-частицы по окружности радиусом R.

На a-частицу также действуют сила тяжести , но она значительно меньше силы Лоренца, поэтому силой тяжести можно пренебречь.

При таком движении a-частицы сила Лоренца является центростремительной.

Скорость, с которой a-частица влетела в магнитное поле, найдем из уравнения движения:

.                                                 (44)

Если векторы равны, то равны и их модули:

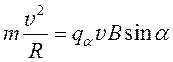,                                             (45)

здесь учтено, что центростремительное ускорение

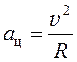.                                                   (46)

Из формулы (46) выразим скорость:

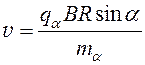.                                              (47)

Подставив в формулу (47) данные задачи, получим:

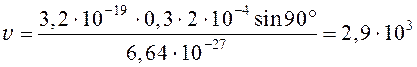(м/с) = 2,9 (км/с).

Период обращения частицы:

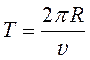.                                                 (48)

Подставим численные значения R и v в формулу (48) и рассчитаем период:

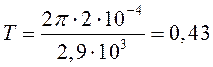 (с).

Ответ: v = 2,9 км/с; Т = 0,43 с.

Задача 6. Электрон, имея скорость 3 Мм/с, влетел в однородное магнитное поле с индукцией 40 мТл под углом 30° к направлению линий индукции. Определить радиус и шаг винтовой линии, по которой будет двигаться электрон.

Дано:

v = 3 Мм/с;

B = 40 мТл;

a = 30°;

qе = 1,6×10-19 Кл;

mе = 9,1×10-31 кг

СИ

3×106 м/с

4×10-2 Тл

Решение.

R– ?

h – ?

На движущийся заряд в магнитном поле действует сила Лоренца:

.                                            (49)

Так как сила Лоренца перпендикулярна вектору скорости, то модуль скорости не будет изменяться под действием этой силы, но при постоянной величине скорости электрона остается постоянным и модуль силы Лоренца. Постоянная сила, перпендикулярная скорости, вызывает движение по окружности. Следовательно, электрон, влетевший в магнитное поле, будет двигаться по окружности в плоскости, перпендикулярной линиям индукции, со скоростью, равной поперечной составляющей  скорости (рис. 16); одновременно он будет двигаться и вдоль поля со скоростью v||:

= v                                                  (50)

v|| =v .                                                 (51)

В результате одновременного движения по окружности и по прямой электрон будет двигаться по винтовой линии.

Радиус окружности, по которой движется электрон, найдем из уравнения движения:

.                                                 (52)

Если векторы равны, то равны и их модули:

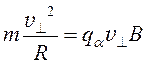,                                            (53)

здесь учтено, что центростремительное ускорение

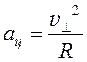.                                                  (54)

Из формул (50) и (53) найдем радиус:

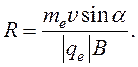                                                 (55)

Подставив в формулу (55) данные задачи, получим:

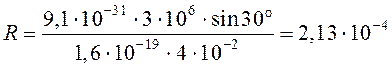= 0,21 (мм).

Шаг винтовой линии h равен пути, пройденному электроном вдоль поля со скоростью v|| за время, которое понадобится электрону для того, чтобы совершить один оборот:

                                                    (56)

где Т - период обращения электрона,

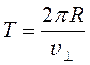.                                                   (57)

Подставив выражения (51) и (57) в формулу (56), получим расчетную формулу для определения шага винтовой линии:

h = 2prctga.                                                (58)

Подставим в формулу (58) численные значения R и a:

 (мм).

Ответ: R = 0,21 мм; h = 2, 3 мм.

3. ПОТОК  ВЕКТОРА  МАГНИТНОЙ  ИНДУКЦИИ.

РАБОТА  ПО  ПЕРЕМЕЩЕНИЮ  ПРОВОДНИКА  И

КОНТУРА  С  ТОКОМ  В  МАГНИТНОМ  ПОЛЕ

Поток вектора магнитной индукции ФВ равен числу линий вектора магнитной индукции, пронизывающих единичную площадку, расположенную перпендикулярно линиям индукции. В СИ магнитный поток измеряется в веберах (Вб).

Скачать файл