Запишем выражение (10) в проекциях на оси х и у:
Bx = B3-B2sina-B1sina; (11)
By = B2cosa-B1cosa; (12)
Bz = 0, (13)
где a = 30°.
Значения магнитных индукций В1, В2 и В3 определим по следующим формулам:
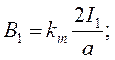 (14)
(14)
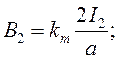 (15)
(15)
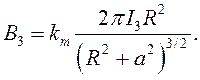 (16)
(16)
Подставив формулы (14), (15) и (16) в выражения (11) и (12), получим систему уравнений:
![]()
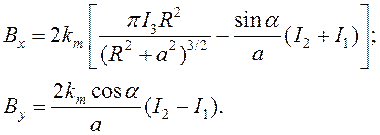 (17)
(17)
Рассчитаем проекции магнитной индукции, подставив данные задачи в выражения (17):
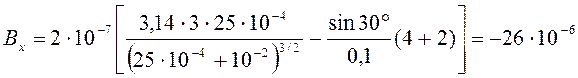 (Тл);
(Тл);
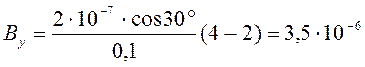 (Тл).
(Тл).
Величина магнитной индукции в точке А может быть определена через ее проекции:
![]() (18)
(18)
![]() (Тл).
(Тл).
Ответ: 1) проекции
вектора магнитной индукции имеют следующие значения: ![]() =
{-2,6 мкТл; 3,5 мкТл; 0}; 2) величина
вектора магнитной индукции В = 4,4 мкТл.
=
{-2,6 мкТл; 3,5 мкТл; 0}; 2) величина
вектора магнитной индукции В = 4,4 мкТл.
Задача 3. Бесконечно длинный проводник с током I1 и контур с током I2 в виде равностороннего треугольника со стороной а расположены так, как показано на рис. 9. Найти магнитную индукцию поля в точке пересечения высот треугольника, если а = 20 см, I1 = 20 А, I2 = 3 А.
|
Дано: I1 = 20A; I2 = 3 A; a = 20 см |
СИ 0,2 м |
|
|
В – ? |
||
По правилу правого винта найдем направления векторов индукции, создаваемых токами I1 и I2. Разобьем контур ECD на три участка (EC, CD и DE) и рассмотрим их как независимые прямые проводники с током конечной длины. Все векторы магнитной индукции перпендикулярны плоскости рис. 9, поэтому координатную ось х удобно выбрать в этом же направлении – «от нас».
Для нахождения магнитной
индукции ![]() в точке А воспользуемся принципом
суперпозиции магнитных полей.
в точке А воспользуемся принципом
суперпозиции магнитных полей.
Запишем принцип суперпозиции в векторном виде:
![]() =
= ![]() +
+![]() +
+![]() +
+![]() .
(19)
.
(19)
Запишем уравнение (17) в проекциях на оси x, y, z:
Вx = В1 + ВЕС + ВCD + BDЕ; (20)
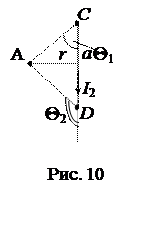 Ву = 0; (21)
Ву = 0; (21)
Вz = 0. (22)
Для определения магнитной индукции ВCD выполним вспомогательный чертеж (рис. 10) и получим:
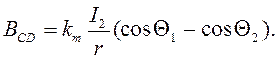 (23)
(23)
Из рис. 9 и 10 видно, что
Q1 = 30°; Q2 = 150°,
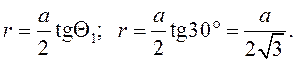
Точка А расположена симметрично относительно одинаковых проводников EC, CD и DE, поэтому согласно формуле (23) индукции магнитных полей, созданных этими проводниками, будут равны, т. е. ВЕС = ВCD = BDЕ.
Вследствие этого формулу (22) можно переписать в виде:
Вx = В1 + 3ВCD. (24)
Магнитную индукцию В1 найдем по формуле:
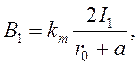 (25)
(25)
где 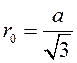 , так
как в точке А высота в равностороннем треугольнике делится в соотношении 2:1
, так
как в точке А высота в равностороннем треугольнике делится в соотношении 2:1
Подставив формулы (24) и (25) в уравнение (23), получим:
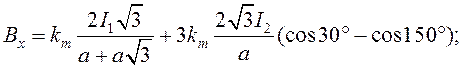 (26)
(26)
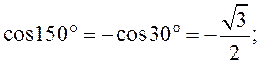
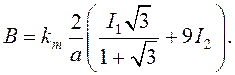 (27)
(27)
Подставив данные задачи в расчетную формулу (27), вычислим величину магнитной индукции в точке А:
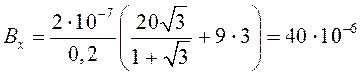 (Тл).
(Тл).
Значение вектора магнитной индукции совпадает со значением проекции Вх.
Ответ: В = 40
мкТл. Проекции вектора ![]() имеют следующие значения:
имеют следующие значения: ![]() = {40 мкТл; 0; 0}. Направление
вектора
= {40 мкТл; 0; 0}. Направление
вектора ![]() совпадает с осью х, которая расположена
перпендикулярно плоскости рис. 9.
совпадает с осью х, которая расположена
перпендикулярно плоскости рис. 9.
2. СИЛА АМПЕРА. СИЛА ЛОРЕНЦА
В магнитном поле на движущийся заряд действует сила Лоренца:
![]() (28)
(28)
где q-электрический заряд;
![]() -его скорость;
-его скорость;
![]() -магнитная индукция внешнего поля.
-магнитная индукция внешнего поля.
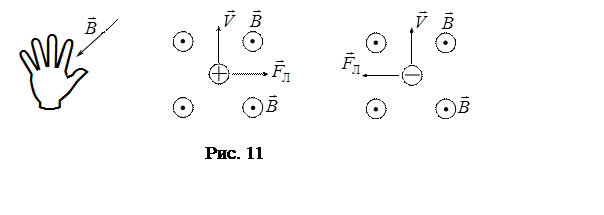 Направление силы Лоренца определяется
исходя из определения векторного произведения или по правилу левой руки (при
этом надо учитывать знак заряда). Это правило заключается в следующем: четыре
пальца левой руки располагают по направлению скорости частицы, при этом линии
магнитной индукции должны входить в ладонь, а отогнутый на 90° большой палец укажет направление
силы Лоренца, действующей на положительно заряженную частицу. Если частица имеет
отрицательный заряд q,
то сила Лоренца направлена в противоположную сторону (рис. 11).
Направление силы Лоренца определяется
исходя из определения векторного произведения или по правилу левой руки (при
этом надо учитывать знак заряда). Это правило заключается в следующем: четыре
пальца левой руки располагают по направлению скорости частицы, при этом линии
магнитной индукции должны входить в ладонь, а отогнутый на 90° большой палец укажет направление
силы Лоренца, действующей на положительно заряженную частицу. Если частица имеет
отрицательный заряд q,
то сила Лоренца направлена в противоположную сторону (рис. 11).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.