Экзаменационные задачи по дисциплине "Теоретические основы электротехники", 3-я часть – электромагнитное поле (с ответами)

Экзаменационные задачи по дисциплине ТОЭ, 3-я часть –

ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ

в 2007/2008 учебном году (с ответами)

Билет №1. Найти силу притяжения обкладок заряженного конденсатора, отсоединенного от источника ЭДС:

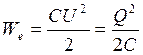, так как Q = UC.

При Q = const

.

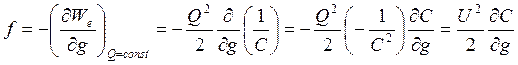Билет №2. Найти силу притяжения пластин конденсатора, подсоединенного к источнику ЭДС:

.

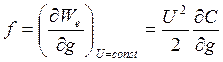Билет №3. Определить величину и направление механических сил, действующих на обкладки цилиндрического конденсатора, если разность потенциалов между электродами равна U = 1000В, радиус внутреннего цилиндра R₁ = 2см, внешнего R₂ = 3см; длина конденсатора  l = 30см, диэлектрическая проницаемость среды e = 2e₀. Краевым эффектом можно пренебречь.

Решение. Определяем обобщенную силу, действующую на внутренний и внешний электроды, через производную по обобщенной координате.

Энергия поля цилиндрического конденсатора

.

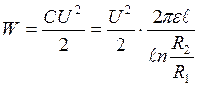Полагая, что разность потенциалов поддерживается постоянной, определим усилие, испытываемое внутренним цилиндром

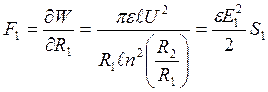, где Е₁ – напряженность поля на поверхности, а   S₁ – площадь электрода.

По своему характеру обобщенная сила представляет здесь растяжение, которое испытывается внутренним цилиндром в направлении увеличения радиуса R₁.

Для внешнего электрода

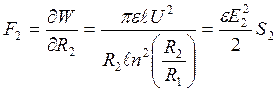
- получаем сжатие в направлении уменьшения радиуса R₂. Численное решение: F₁  5 ×10^-3 Н,    F₂  3,4 ×10^-3 Н;

Билет №4. Измерительный механизм электростатического вольтметра состоит из двух пар металлических секторов, между которыми вращается легкий металлический бисквит. Он также состоит из двух секторов несколько меньшего диаметра. Зазор между подвижной и неподвижной пластинами равен d, радиус бисквита равен R₀, диэлектрическая проницаемость среды e₀ (рис.). Полагая, что противодействующий момент растяжек, на которых подвешен бисквит, равен

М_пр = ba,

а емкость между подвижной и неподвижной пластинами в первом приближении можно определить по формуле для плоского конденсатора, найти выражение для чувствительности вольтметра .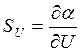

Решение. В данном случае обобщенной координатой является угол поворота бисквита относительно неподвижных пластин a, а обобщенная сила представляет собой вращающий момент М_вр. Равенство вращающего и противодействующего моментов позволит определить искомое выражение для чувствительности.

Для решения задачи воспользуемся положением, что производная от энергии поля системы по обобщенной координате дает обобщенную силу.

Приближенное значение емкости системы при произвольном угле a

.

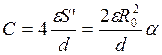Энергия поля, запасенная в конденсаторе,

.

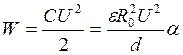При заданной разности потенциалов U вращающий момент, действующий на бисквит,

;

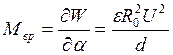в положении равновесия М_вр = М_пр

.

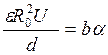Отсюда чувствительность вольтметра

.

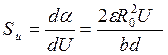Билет №5. Плоский конденсатор с многослойным диэлектриком имеет площадь обкладок S = 25см², толщины слоев d₁ = 2см, d₂ = 3см, d₃ = 2см и удельные проводимости в слоях:

g₁ = 10^-10 1/Ом×м; g₂ = 1,5 ×10^-10 1/Ом×м; g₃ = 10^-10 1/Ом×м. Определить сопротивление утечки и емкость конденсатора, используя метод электростатической аналогии.

Решение. Электрический ток проводимости в конденсаторе вследствие конечной проводимости диэлектриков одинаковый во всех слоях

I = JS, т.к. S одинаково, то и J одинаково во всех слоях, поэтому

;   ;     ;

;

.

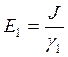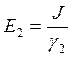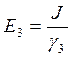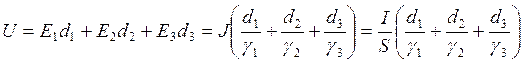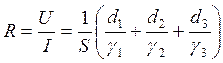Проводимость утечки G_ут = , откуда

.

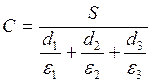Билет №6. Коаксиальный кабель имеет радиус прямого провода (жилы) r₁ = 1см; внутренний радиус обратного провода (оболочки) r₃ = 3см. Изоляция состоит из двух слоев. Граничная поверхность между ними имеет радиус r₂ = 2см. Удельная проводимость слоев: g₁ = 10^-10 1/Ом×м; g₂ = 2 ×10^-10 1/Ом×м. Определить сопротивление утечки R_ут и емкость кабеля на 1 км длины.

Решение. По аналогии с предыдущей задачей

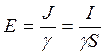
, где I – ток утечки, S = 2prl - поверхность цилиндра.

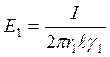 - напряженность поля на внутренней границе 1-го слоя.

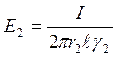 - то же на внутренней границе 2-го слоя (рис.2.3).

Напряжение между проводами кабеля

;

.

; .

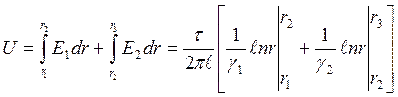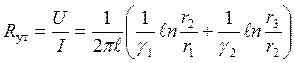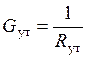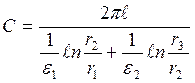Билет №7. Плоский конденсатор с двухслойным диэлектриком d₁ = d₂ = 1 см;      подключен к источнику постоянного напряжения 3 кВ. Требуется: 1) Определить напряженность поля, сопротивление конденсатора и мощность, выделяющуюся в единице объема диэлектрика, а также свободный и связанный поверхностные заряды на границе слоев. 2) Как изменится решение задачи, если диэлектрик будет идеальным ()?

Решение. По определению напряжение ; граничное условие  (т.е. ). Из двух уравнений находим ;  ;           ;          ;  ;            ; . Тогда ; , где  - в Ф/см. Потери активной мощности в единице объема  и .

Сопротивление конденсатора на единицу площади пластин . При  по-прежнему ; граничное условие , т.е. . Из двух уравнений получим     ; ;

 ;   ;   .

Билет №8. На глубине h под поверхностью земли (рис.1) находится сферический электрод (проводимость g₃) радиусом , к которому подводится постоянный ток I по изолированному вертикальному кабелю. Требуется найти магнитное поле в земле и воздухе, считая проводимость земли g постоянной. Второй электрод расположен далеко от первого – на расстоянии, значительно превышающим h.

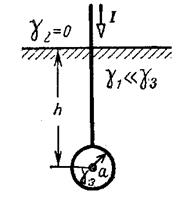
Рис.1

Решение. Для определения плотности тока в земле можно пользоваться методом зеркальных изображений: влияние границы раздела сред (поверхности земли) заменяем током I’ = I фиктивного электрода (рис.2). Применяя принцип наложения, определим магнитное поле в земле. Поле истинного тока с напряженностью:

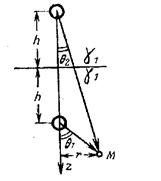
Рис.2

.

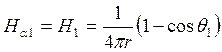Поле изображения тока

.

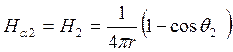Общее магнитное поле в земле

.

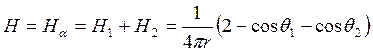Магнитное поле в воздухе по-прежнему . На границе ( получаем .