Электротехника \ Теоретические основы электротехники

Экзаменационные задачи по дисциплине "Теоретические основы электротехники", 3-я часть – электромагнитное поле (с ответами), страница 3

Таким образом, скалярные магнитные потенциалы определены:

;

;

.

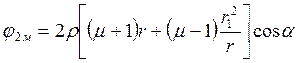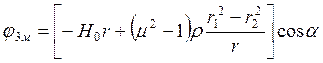Теперь можно определить напряженность магнитного поля в каждой области:

1)  Внутри трубы

, т.е. внутри трубы магнитное поле однородно (при однородном внешнем поле с напряженностью Н0).

2)  В стенке трубы

;

;

3)  Вне трубы

;

.

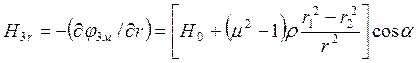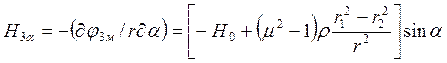Коэффициент экранирования

.

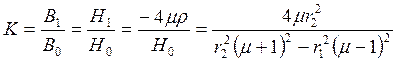Если , то .

Билет №12. Определить силу, действующую на частицу с зарядом Q = 1,6 ×10-19Кл, движущуюся в магнитном поле с индукцией В = 1,5Тл. Частица движется со скоростью v = 2,5 ×106 м/с под углом a = 45° к направлению вектора магнитной индукции.

Решение.

, Н.

Так как заряженная частица движется под углом к направлению магнитного поля, то ее траектория представляет собой винтовую линию. При движении заряженной частицы под прямым углом к направлению магнитного поля ее траектория была бы окружностью в плоскости, нормальной к магнитному полю.

Билет №13. Плоскость рамки составляет угол a = 30 ° с направлением однородного магнитного поля в воздухе с индукцией B = 0,1 Тл (рис.1). Площадь рамки S = 100см2. Число витков w = 50, ток в рамке I = 4А. Определить вращающий момент рамки.

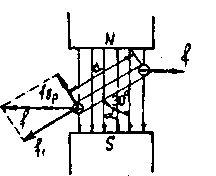
Рис.1

Решение. Сила, действующая на сторону рамки,

f = ВIlw,

где l - длина рамки.

Вращающий момент рамки

Мвр = f, где - ширина рамки.

.

Наибольший вращающий момент у рамки будет при  = 0, когда она займет вертикальное положение, наименьший вращающий момент, равный нулю, будет при горизонтальном положении рамки. Рамка с постоянным током стремится занять такое положение, при котором ее пронизывает максимальный магнитный поток.

Билет №14. Расстояние между проводами d = 10 см (рис.1). Токи в проводах I1 = 1000А, I2 = 500А направлены в одну сторону. Длина проводов 1м. Определить магнитную силу взаимодействия f.

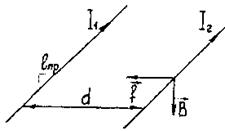
Рис.1

Решение.

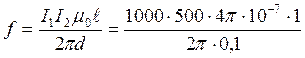=1 Н.

Провода притягиваются.

Билет №15. По двум параллельным проводам двухпроводной линии протекают равные по величине, но противоположно направленные токи I1 = I2 = 400А. Расстояние между осями проводов d = 0,3м. Найти величину и направление магнитной силы, действующей на 1 км длины каждого провода.

Решение:

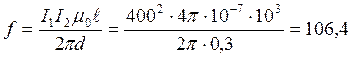 Н.

Эти силы отталкивают провода.

Билет №16. Два длинных провода с пренебрежимо малым сопротивлением замкнуты с одного конца на сопротивление R, а с другого конца подключены к источнику постоянного напряжения (рис.1). Радиус сечения каждого провода r0 в 20 раз меньше расстояния между осями проводов . При каком значении сопротивления R результирующая сила взаимодействия проводов обратится в нуль?

Рис.1

Решение. На каждом из проводов (протекает по ним ток или нет) при подключении их к источнику напряжения имеются свободные заряды. Линейная плотность зарядов 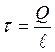. Поэтому кроме магнитной силы fм необходимо учесть и электрическую fэ. Электрическая сила fэ, действующая на единицу длины провода со стороны другого провода

fэ  = tЕ.

Величина Е равна

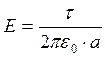, поэтому

.

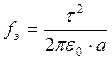Магнитная сила fм на единицу длины провода

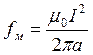, где I – сила тока в проводе.

Обе силы – электрическая и магнитная – направлены в противоположные стороны: электрическая сила обусловливает притяжение проводов, магнитная – их отталкивание. Отношение сил

.

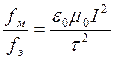Билет №17. Вдоль длинного тонкостенного круглого цилиндра радиуса R течет ток I. Какое давление испытывают стенки цилиндра?

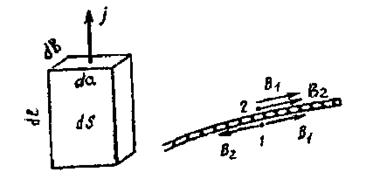
а)                                 б)

Рис.1

Решение. Рассмотрим поверхностный элемент тока I'dS, где I' – линейная плотность тока (I' = , где l - длина цилиндра), dS – элемент поверхности цилиндра (рис.1). При этом

.

Смысл входящих сюда величин пояснен на рис.1,а. В векторном виде

   .

Сила Ампера, действующая на поверхностный ток с учетом последнего выражения,

, где  - магнитная индукция поля в месте нахождения рассматриваемого элемента тока от всех других элементов тока, исключая данный.

Определим величину . Пусть В2 – магнитная индукция, создаваемая самим элементом тока. Для магнитного поля плоскости с током мы получили

Скачать файл