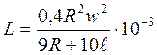Экзаменационные задачи по дисциплине "Теоретические основы электротехники", 3-я часть – электромагнитное поле (с ответами), страница 5

, где R – радиус витков; l - длина катушки; w – число витков катушки.

Определить: силу, сжимающую катушку и стремящуюся разорвать виток катушки (увеличить ее радиус) при I = 2,45А, R = 0,05м,  l = 0,2м, w = 100.

Решение. Сила, сжимающая катушку,

Знак (-) указывает на то, что сила сжимает катушку.

Сила стремящаяся разорвать витки,

.

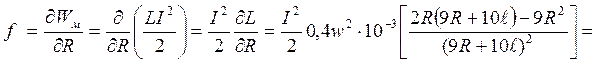
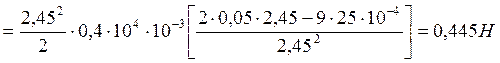Знак (+) - сила положительна, направлена наружу.

Билет №22. При изменении расстояния x между контурами, показанными на рис.1, коэффициент связи изменяется по закону k = , где А = 2см³. Найти силу взаимодействия обоих  контуров при х = 3см, если L₁ = 0,4мГн, L₂ = 6,25 мГн, I₁ = I₂ = 100 A. Токи I₁ и I₂ имеют одинаковое направление.

Рис.1

Решение. Так как заданы токи контуров, то пользуемся формулой

.

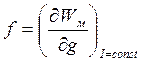Энергия системы двух контуров

;

;

.

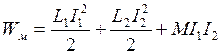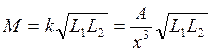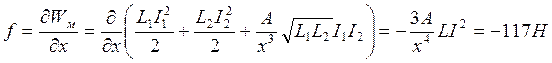Отрицательный знак указывает на то, что контуры притягиваются.

Билет №23. По обмотке стального тороида с числом витков w = 400 проходит ток I = 4А. Площадь сечения сердечника S = 4см². В сердечнике имеется воздушный зазор d = 2 мм. Определить силу, с которой притягиваются торцы сердечника, считая магнитное поле в зазоре однородным, а магнитную проницаемость стали бесконечно большой (m_r  = ¥).

Решение. Силу будем определять по формуле Максвелла

   .

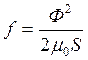Магнитный поток

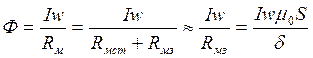, где 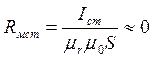 - магнитное сопротивление стали,

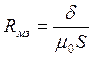   - магнитное сопротивление зазора.

.

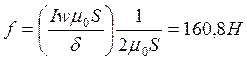Билет №24. Электромагнит, показанный на рис.1, имеет площадь каждого полюса S = 0,01м², индукцию при притянутом якоре В = 1Тл. Определить подъемную силу электромагнита, т.е. силу отрыва якоря от полюсов.

Рис.1

Решение.

= .

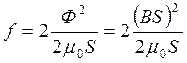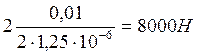Цифра 2 перед дробью объясняется тем, что силу притяжения создает каждый полюс, а всего их два.

Билет №25. Имеется контур с током, у которого АВ – подвижная перемычка (рис.1). Индуктивность этого контура зависит определенным образом от координаты х, т.е. известно L(x). Найти силу Ампера двумя способами: при I = const и при  Ф = const.

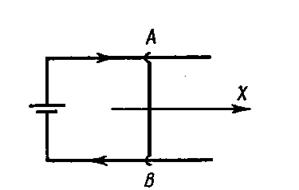
Рис.1

Решение. Магнитная энергия системы

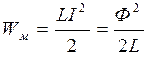   , где Ф = LI. Переместим перемычку, например, вправо на dx. Так как dA_мех = fxdx, то

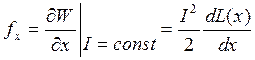, или

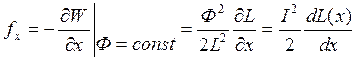, т.е. расчет по обеим формулам дает один и тот же результат.

Билет №26. Определить магнитное давление на обмотку соленоида.

Решение.      Увеличим мысленно радиус сечения соленоида на dr, сохранив при этом неизменным ток через обмотку. Тогда силы Ампера совершат работу dA_мех = 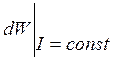. В нашем случае

dA_мех = pSdr, где р – искомое давление, S – боковая поверхность соленоида;

dW_|I=const = .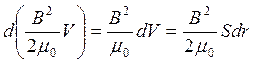

Здесь учтено, что при I = const и B = const. Из  равенства двух последних выражений находим

.

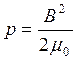Билет №27. При поражении молнией трубчатого молниеотвода труба оказалась сплющенной. Требуется определить давление, действовавшее на трубу при токе молнии I = 200000A, в предположении, что ток протекал лишь в тонком поверхностном слое трубы (скин-эффект). Наружный радиус трубы r₀ = 1,25см.

Решение. Силу, с которой магнитное поле действует на поверхность трубы, определим из выражения , где h - обобщенная координата,  - составляющая силы по этой координате. Применим это выражение к силе, действующей на элемент поверхности, . Так как ток сосредоточен на поверхности трубы, то магнитное поле отлично от нуля лишь вне трубы.

Если элемент поверхности под воздействием силы перемещается на dr, то приращение энергии магнитного поля

, и сила, действующая на элемент поверхности dS,

Давление

.

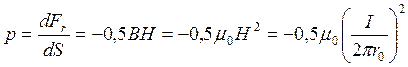Знак минус указывает на то, что сила стремится уменьшить радиус, т.е. сжимает трубку. Подставляя числовые данные, получаем

.

Билет №28. На рис.1 схематически показан якорь электрической машины, имеющей всего один виток. Продольная длина якоря  l = 0,5м, наружный диаметр якоря = 0,2м, диаметр окружности, на которой расположены провода, d = 0,16м. Магнитная проницаемость стали = 500. Ток в витке I = 50А. Требуется определить значение вращающего момента М, действующего на якорь, оценить силу F, действующую на провода, и момент, обусловленный давлением проводов, М₀, считая магнитное поле под полюсами однородным с индукцией В = 1Тл (при токе в витке, равном нулю).