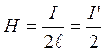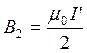Экзаменационные задачи по дисциплине "Теоретические основы электротехники", 3-я часть – электромагнитное поле (с ответами), страница 4

,      .

Далее, воспользовавшись законом полного тока и соображениями симметрии, легко установить, что снаружи цилиндрической поверхности

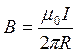, внутри нее В = 0.

Согласно рис.1,б (ток течет от нас), в точке 1  В = В₁  - В₂ = 0; в точке 2 В = В₁ + В₂ =  , откуда В₁ = В₂ = .

Подставив этот результат в выражение для силы, получим искомое давление

,

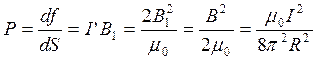(здесь I¢ выражено из В₁ = ).

Из выражения для силы видно, что сила  направлена внутрь цилиндра, т.е. цилиндр испытывает боковое сжатие.

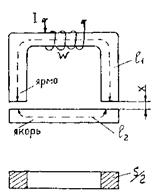
Билет №18. Якорь электромагнита удален на расстояние х от ярма. В магнитной системе образовано два зазора. Длина каждого из них х, поперечное сечение S/2 (рис.1). Энергия магнитного поля  в каждом зазоре равна произведению плотности энергии BH/2 на объем зазора (S/2 × х), так как магнитное поле в зазоре считается однородным.

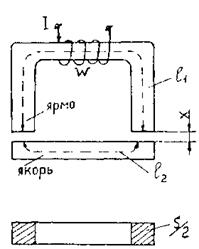
Рис.1

Решение. Поскольку участки по стали имеют проницаемость в тысячи раз большую, чем в зазоре, то при не очень малых зазорах при B = const H_з >>H_ст, энергия магнитного поля в зазоре много больше энергии магнитного поля в сердечнике (W_мз >> W_{м ст}) т.е.

W_м = W_мз +  W_{м ст}  W_мз.

При притяжении якоря электромагнита к ярму меняется магнитное сопротивление, магнитный поток и потокосцепление. Ток в обмотке электромагнита не меняется (если электромагнит подключен к источнику постоянного напряжения), поэтому для определения силы f пользуемся выражением

.

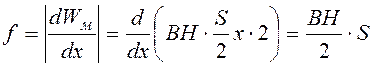Формула совпадает с формулой Максвелла

.

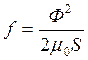Действительно,

.

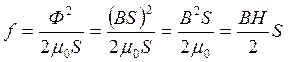Фактически объяснить притяжение якоря к ярму можно следующим образом: электрический ток в цепи замыкается по пути (или через участки) наименьшего сопротивления. Магнитный поток в магнитной цепи также стремится замкнуться по пути наименьшего сопротивления. Если магнитная цепь стационарна, потоки просто замыкаются по таким путям. Если в магнитной цепи имеются определенные степени свободы, позволяющие уменьшить магнитное сопротивление, это происходит следующим образом: якорь притягивается к ярму, сердечник втягивается внутрь катушки (см. ниже).

При В = 1,5 Тл, S = 20 см².

;

.

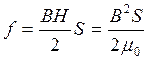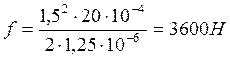Билет №19. Сопротивление R обмотки электромагнита (w=1000) равно 9,8Ом. Пренебрегая потоком рассеяния и выпучиванием потока в зазоре, определить величину ЭДС источника (постоянного или переменного напряжения), при которой якорь электромагнита будет  притягиваться к ярму с силой f = 100кг (981 Н); S = 20см²; l₁= 55 см; l₂ = 15см; х = 2мм (см. рис.1. Якорь и ярмо изготовлены из магнитно-мягкого материала с кривой намагничивания, изображенной на рис.2.

Рис.1

Рис.2

Решение. Согласно

.

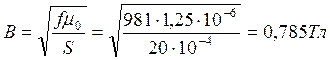По закону полного тока (второму закону Кирхгофа для магнитной цепи)

;

.

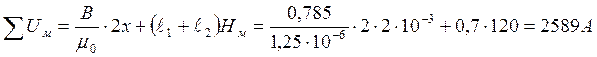Здесь 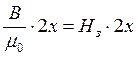- магнитное напряжение в зазорах; (l₁+l₂)Н_м – магнитное напряжение в ярме и якоре; Н_м – напряженность магнитного поля в магнитопроводе (в ярме и якоре), определяется по кривой намагничивания соответственно индукции В = 0,785Тл, Н_м = 120А/м.

Ток в обмотке

.

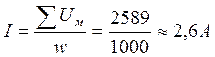Если ЭДС Е постоянна во времени, то

Е = IR = 2,6 × 9,8 » 25 В.

Если ЭДС Е переменна, т.е. е = Е_msin w t , где w = 314 (w = 2pf,  f = 50Гц), то

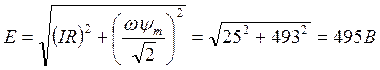, здесь IR – падение напряжения на активном сопротивлении обмотки электромагнита;

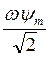- падение напряжения на индуктивном сопротивлении электромагнита. Действительно, .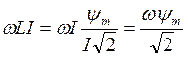

Амплитуда потокосцепления

;

.

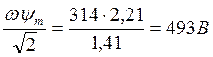Билет №20 По круглому медному витку радиусом R толщиной 2r (рис.1) протекает ток I. Индуктивность витка определяется по формуле

.

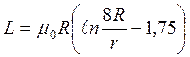Определить механические силы, действующие на виток.

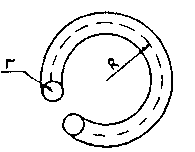
Рис.1

Решение. При постоянном токе в витке

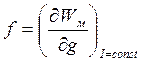, где g – обобщенная координата. В рассматриваемом случае обобщенными координатами являются R и r.

.

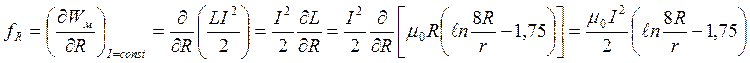Сила f_R > 0. Она стремится увеличить радиус витка R, т.е. растянуть  контур с током и увеличить индуктивность витка L.

.

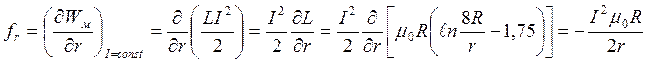Сила f_r < 0. Она стремится уменьшить радиус провода (за счет этого и растягивается контур) и увеличить индуктивность витка L.

Билет №21. Индуктивность однослойной короткой катушки приближенно определяется выражением, Гн,